混合正規分布モデル

ここでは，MClustパッケージを使った混合正規分布モデル (Gaussian Mixture Model, GMM) のフィッティングの方法を解説します。

準備

本ページで使用するパッケージがインストールされていない場合は，以下のコマンドをコンソールに入力してインスト―ルしてください。

install.packages("mclust")
install.packages("mvtnorm")

以下の2行で必要なパッケージを読み込みます。

library(mvtnorm)
library(mclust)

データの生成

ここでは，混合正規分布モデルから人工データを生成します。 データは3つのコンポーネントからなる，2次元の混合正規分布から 生成します。

# 乱数のシードを設定
set.seed(1)

# サンプル数
n.sample <- 1000

# 各コンポーネントの平均，分散・共分散行列を設定
true_means <- list(c(0,4),   # コンポーネント1の平均ベクトル
                   c(-3,-1), # コンポーネント2の平均ベクトル
                   c(3,-1)   # コンポーネント3の平均ベクトル
                   )
true_sigmas <- list(diag(2), # コンポーネント1の分散・共分散行列
                    diag(2), # コンポーネント2の分散・共分散行列
                    diag(2)  # コンポーネント3の分散・共分散行列
                    )
# 混合比を設定
true_pi <- c(0.4,0.3,0.3)

# データを生成
dat <- matrix(0,nrow = n.sample, ncol = 2) 
for (idx in 1:n.sample) {
  # 選択するコンポーネントのインデックスを決定
  idxk <- which.max(rmultinom(1,1,true_pi))
  dat[idx,] <- rmvnorm(n = 1,
                      mean = true_means[[idxk]],
                      sigma = true_sigmas[[idxk]]  )
}

# データをデータフレームに格納
df_data <- data.frame(dat)

実際は上のような人工データを作るときは， 毎回混合比に従う乱数を発生させるのではなく， サンプル数×混合比の数のサンプルをそれぞれのコンポーネントに 対応する正規乱数から発生させ，まとめるということが 行われます。ここでは混合正規分布モデルに忠実に データを生成しました。

データの確認

データが正しくデータフレームに格納されているか，以下で確認します。

dim(df_data)

## [1] 1000    2

head(df_data,5)

X1	X2
3.1836433	-1.835629
0.4146414	2.460050
-3.2947204	-1.005767
-0.3053884	5.511781
-1.1476570	3.710538

データをプロットする

生成したデータを以下でプロットしてみます。

par(pty = "s")
plot(df_data$X1, df_data$X2, pch=".",cex = 2, xlab="X1", ylab="X2")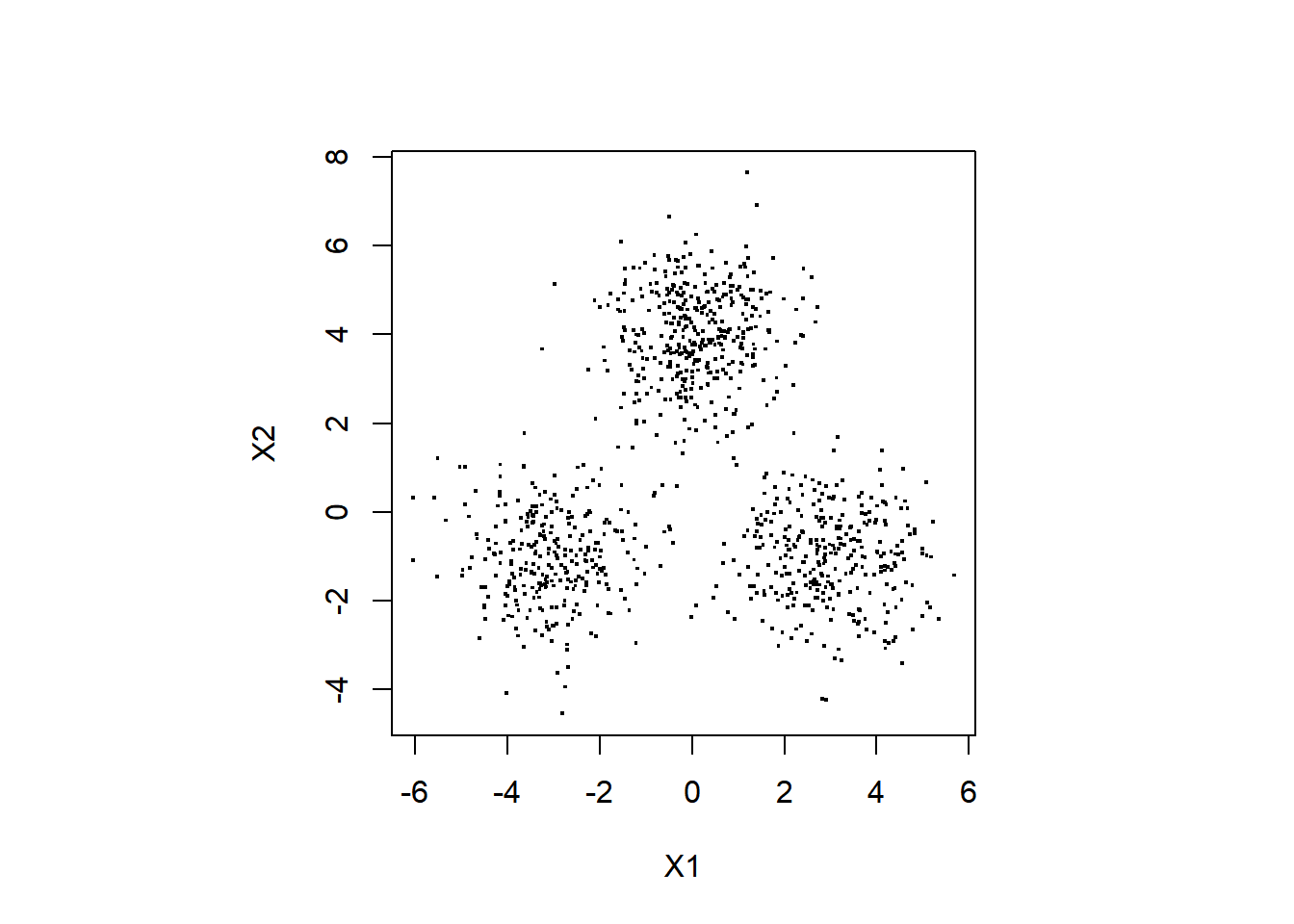

MclustによるGMMのフィッティング

ここでは，コンポーネント数を3に指定して 関数MclustでGMMのフィッティングを行います。

mod1 <- Mclust(df_data, # データ
               G = 3, # コンポーネント数
               modelNames = "VVI" # モデルの分散・共分散行列の構造の指定 (VVIは制約のない通常のGMM)
               )

フィッティングの結果の表示

以下で，GMMの結果を表示します。

par(pty = "s")
plot(mod1, what = "classification")

データ生成に用いた真のモデルに対応する3つのコンポーネントが推定され，各サンプルが適切にクラスタリングされていることがわかります。 (各サンプルが所属するクラスターで色分けされています。

以下で推定されたパラメータの値なども表示されます(長いので省略)。

summary(mod1, parameters = TRUE)

コンポーネント数の選択

次にコンポーネント数をBICを用いて データから選択する方法を試します。 (混合正規分布モデルのような非正則なモデルでは BIC導出時になされる近似の前提が成り立たないため，本来は ここでBICを使うのは適切ではないとされます。 しかし，それでもパラメータ数でペナルティを与える方法の 一つと割り切ってか，実際にはよく用いられるようです。)

BIC <- mclustBIC(df_data, 
                 G = 1:8, # 候補となるコンポーネント数
                 modelNames = "VVI"
                 )
plot(BIC)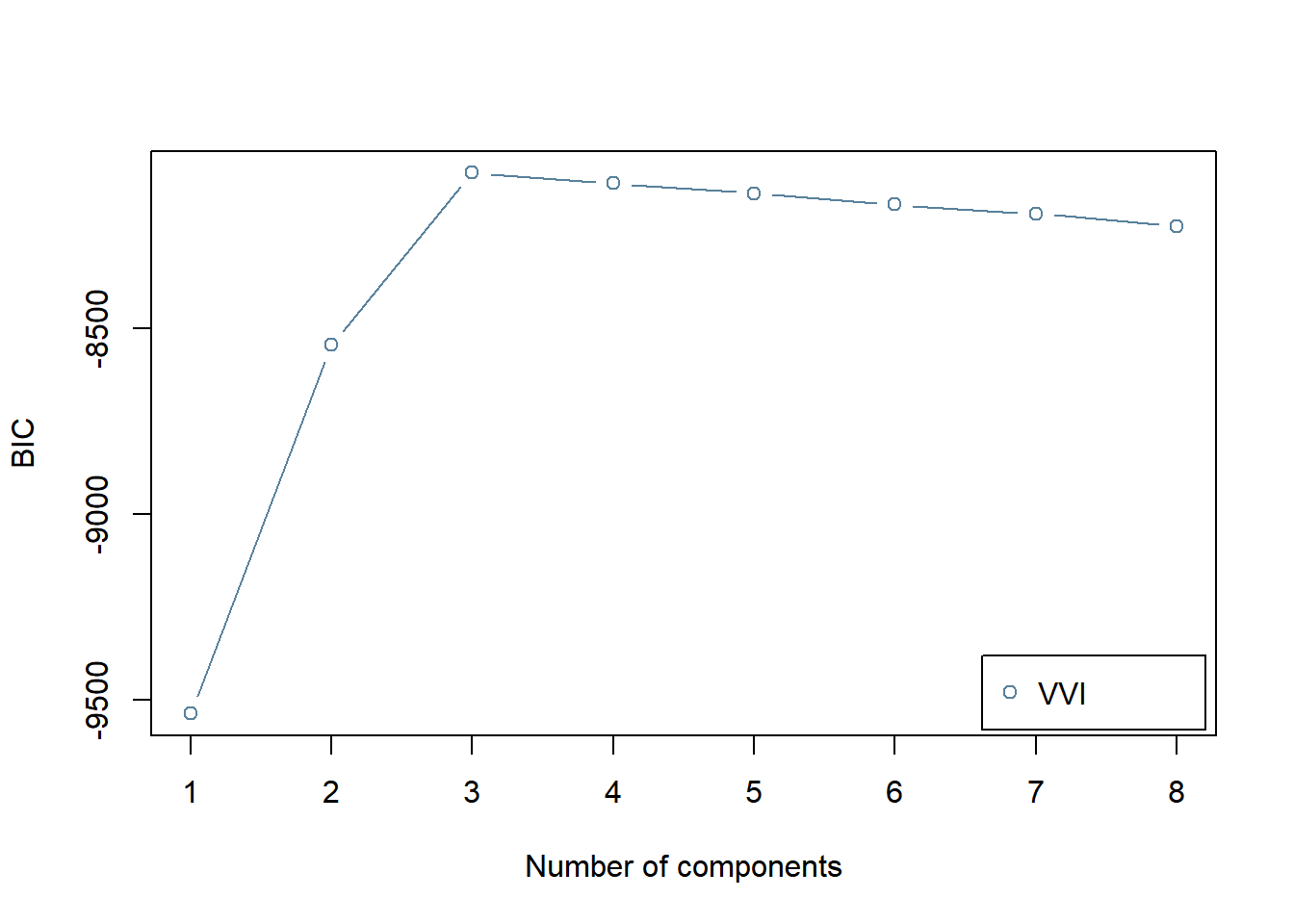

BICは標準的には小さい方が良いモデルとなる指標なのですが， MClustでは符号が逆になり，大きい方が良いモデルとなるようにしているようです。真のモデルと同じ，コンポーネント数が3のときにBICの値が最大となり，最適なモデルとして選択されます。

BICで選択されたモデルでモデルフィッティングをするときは以下のようにします。

mod2 <- Mclust(df_data, x = BIC)

上は，コンポーネント数を3としてフィッティングしたmod1と 同じ結果が得られます (結果は省略)。