実データ (Johnson-300) の解析1

準備

本ページで使用するパッケージがインストールされていない場合は，以下のコマンドをコンソールに入力してインスト―ルしてください。

install.packages("psych")
install.packages("GPArotation")
install.packages("tidyverse")
install.packages("GGally")

必要なパッケージを読み込みます。

library(psych)
library(GPArotation)
library(tidyverse)
library(GGally)

ここでは，Gerlachらにならい，Johnsonにより公開されている，パーソナリティに関する300項目の質問への回答データ (IPIP-NEO-300) を読み込み，因子分析まで行います。この質問項目の並びは IPIP-NEO-ItemKey.xls で確認することができます。 1項目から順に，神経症傾向 (N), 外向性 (E), 開放性 (O), 協調性 (A) , 誠実性 (勤勉性) (C)に関する質問項目が並び，それが60周するまで，計300項目並べられています。

データファイルIPIP300.datはJohnson’s IPIP-NEO data repository (https://osf.io/tbmh5/) からダウンロードできます。ここでは，このファイルを“C:/data/personality/IPIP300.dat” においてあるものとしています。以下のスクリプトのパスは適宜ご自身の環境に合わせて書き換えてください。

データの読み込み

IPIP300.datは固定長データ形式で納められています。

nmax <- Inf # 読み込む最大行数 最初は小さくして試す

dat.raw <- scan(file = "C:/data/personality/IPIP300.dat", 
          nmax = nmax,
          what = character(), sep = "\n")

n.data <- length(dat.raw)
dat.matrix <- matrix(0,nrow = n.data, ncol = 300)

n.used.data <- 0
for (idx in 1:n.data){
  
  # 回答があるのは34列目から333列目　
  # そこを抜き出す
  a <- substring(dat.raw[[idx]],34, 333)
  
  a.numeric <- as.numeric( unlist(strsplit(a,"")))
  
  # 一つでも無回答 (0) がある回答者は除外する
  if (!any(a.numeric == 0)) {
    n.used.data <- n.used.data + 1
    dat.matrix[n.used.data,] <- a.numeric 
  }
}

# 不要な行は削除
df_data <- as.data.frame(dat.matrix[1:n.used.data,])

“N”の項目 (1, 5, 10,…,296), “E”の項目(2, 6, 11,…,297), “O”の項目(3, 7, 12,…,298), “A”の項目(4, 8, 13,…,299), “C”の項目(5, 9, 14,…,300), の順番になるよう列を並び替えます。

# 並べ替えのためのインデックス
idxseq <- c(seq(1,300, by=5), # N
         seq(2,300, by=5), # E
         seq(3,300, by=5), # O
         seq(4,300, by=5), # A
         seq(5,300, by=5) # C
)

df_data <- df_data[,idxseq]

因子分析

因子数の検討

Gerlachらにならい，Big fiveモデルに基づいて因子数は5にしますが，ここではスクリープロットも見てみます。

VSS.scree(df_data)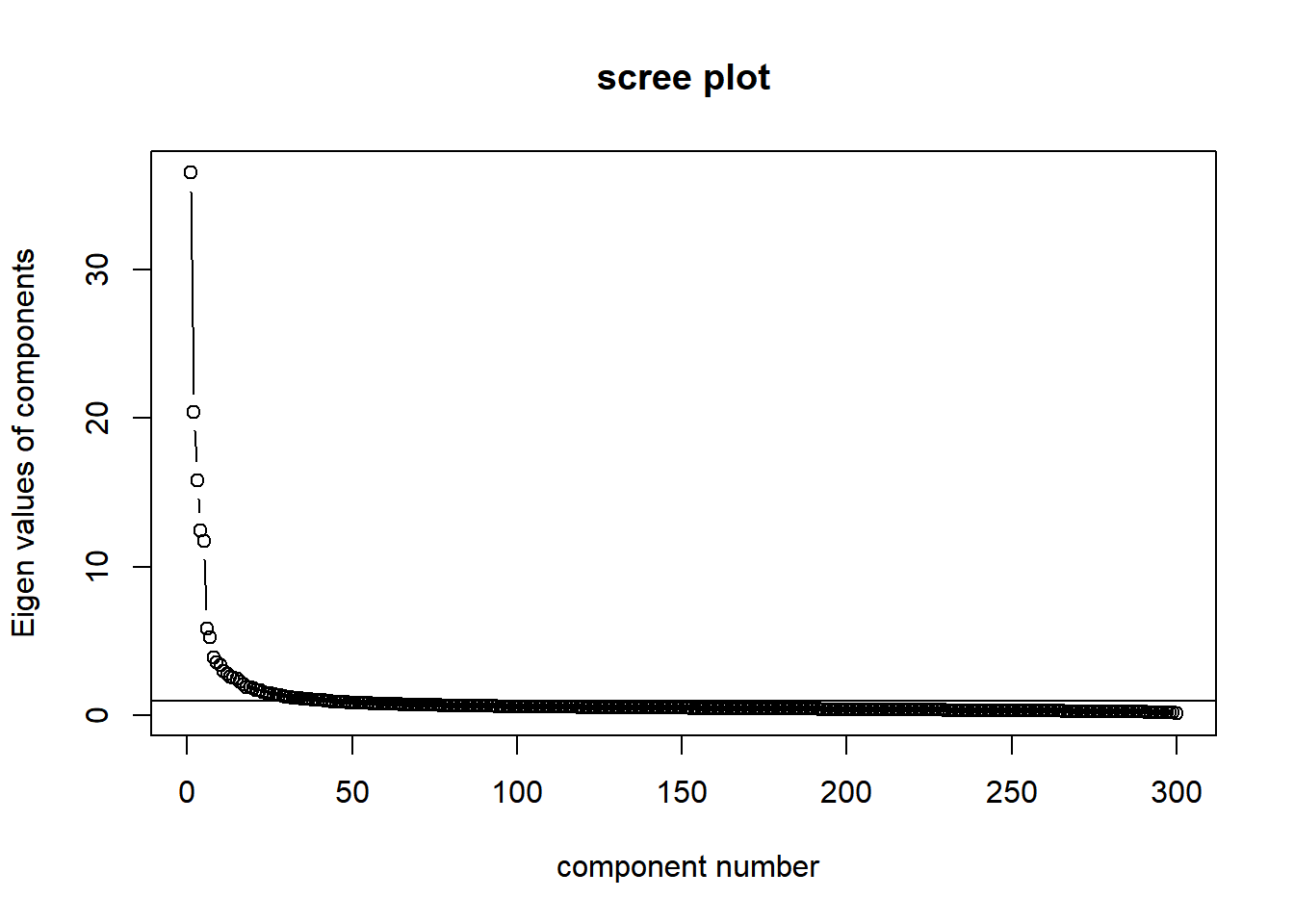

第6固有値以降で減少幅が小さくなっていると見えなくもないでしょうか。

因子負荷，因子スコアの推定

最尤法とバリマックス回転で因子分析を行い，推定された因子スコアをデータフレームdf_scに格納します。

res_fa <- fa(df_data, nfactors = 5, rotate = "varimax",  fm = "ml")

# 因子スコアをHermanの方法で推定する
fsc <- factor.scores(df_data, f = res_fa, method = "Harman")

# 推定された因子スコアをデータフレームに
df_sc <- data.frame(fsc$scores)

因子の解釈

因子負荷は以下のようになります。(19/09/18 全体の因子負荷を見て因子のラベルを決めるように修正しました)

cor.plot(res_fa, numbers = F)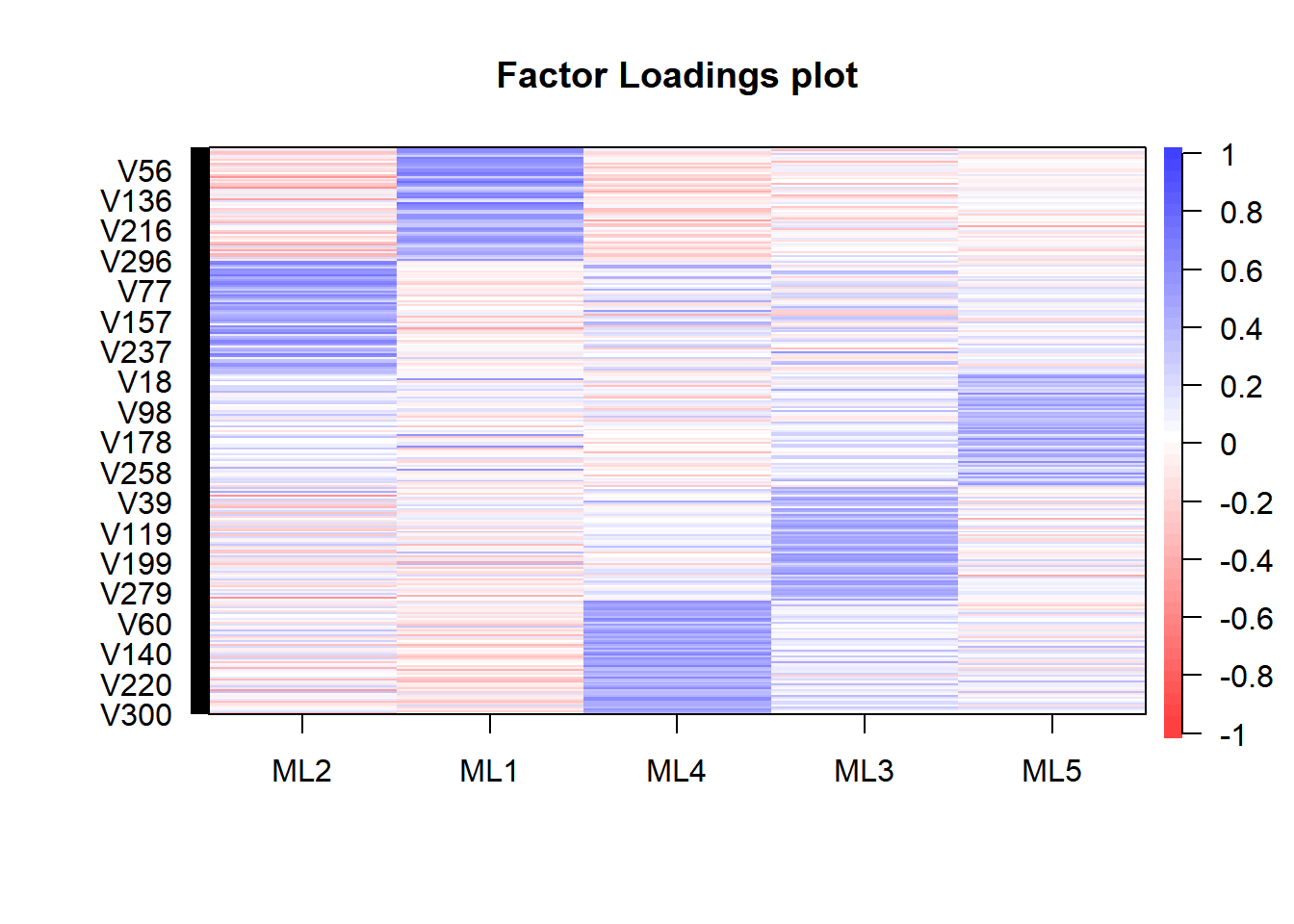

それぞれの因子は以下の項目に高い因子負荷を持っていることがわかります。 (上でN, E, O, A, Cがそれぞれ60項目繰り返されて順に並ぶように項目を並び替えたのでした。)

1番目の因子 (ML2) は外向性 (E)
2番目の因子 (ML1) は神経症傾向 (N)
3番目の因子 (ML4) は誠実性 (C)
4番目の因子 (ML3) は協調性 (A)
5番目の因子 (ML5) は開放性 (O)

これをもとに推定された因子スコアにラベルを付けます。

names(df_sc) <- c("E","N","C","A","O")

# 順番を元のデータの並びに合わせるように列を並び替える
df_sc <- df_sc[,c("N","E","O","A","C")]

推定された因子スコアをプロットしてみます。ここではggplotとggpairsを使います。

# 2次元周辺分布の密度の等高線プロット用の関数
my_fn <- function(data, mapping, ...){
  g <- ggplot(data = data, mapping = mapping) + 
    stat_density2d(aes(fill=..density..), geom="tile", contour = FALSE) +
    geom_density2d(color = "black")  + 
    scale_fill_gradientn(colours=viridis::viridis(100, option="viridis"))
  g
}

ggp <- ggpairs(df_sc, 
        lower=list(continuous=my_fn))

print(ggp)

これはGerlach et al. (2018)のSupplementary Figure 2に対応する図です。見比べると，分布の形状が一致していることが確認できます。

因子スコアのcsvファイルへの書き出し

次の解析のため，因子スコアを以下のようにcsv形式で保存しておきます。

 write.csv(df_sc, "C:/data/personality/fs_IPIP300.csv", 
             row.names = FALSE)

このデータは，以下のように読み出せます。

df_data <- read.csv("C:/data/personality/fs_IPIP300.csv", header = TRUE)

また，このcsvファイルはこちらにもアップロードしておきます。

(実データ (Johnson-300) の解析2 へ)