ここでは，Gerlachらの分析法で紹介した関数を使ってGerlachらの分析を行う方法を例示します。

準備

本ページで使用するパッケージがインストールされていない場合は，以下の コマンドをコンソールに入力してインスト―ルしてください。

install.packages("psych")
install.packages("GPArotation")
install.packages("ks")
install.packages("mclust")
install.packages("tidyverse")

必要なパッケージを読み込みます。

library(psych)
library(GPArotation)
library(ks)
library(mclust)
library(tidyverse)

クラスター評価のための関数を読み出します。

source("functions_component_evaluation.R")

このRスクリプトはこちらからダウンロードできます。

データの読み込み

こちらで作成したデータdata_fa_GMM1.csvをデータフレームdf_dataに読み出します。

df_data <- read.csv("./data_fa_GMM1.csv", header = TRUE)
head(df_data,5)
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
5.369310 1.480908 0.3204278 -1.3496938 1.759920 1.3164542 4.2853056 5.7518398 4.853400 4.436487
8.385332 6.966283 8.3258330 9.6991964 11.668750 -0.2588496 0.1533774 -0.0647089 -1.045956 -2.503212
-3.691115 -3.356659 -3.6179367 -0.0886347 -5.675790 0.4823171 -0.1155893 0.3087366 -1.112879 -4.384141
3.019875 6.597137 3.9982466 11.0006238 3.851946 -1.6343137 0.3125354 -0.1176835 -0.420932 -1.309458
-3.313268 -6.302669 -5.0662851 -10.1785300 -9.816317 -0.6429079 1.4148340 -0.1015601 -1.810785 -0.808941

探索的因子分析の実行

因子数を決める

スクリープロットで因子数を決めます。

VSS.scree(df_data)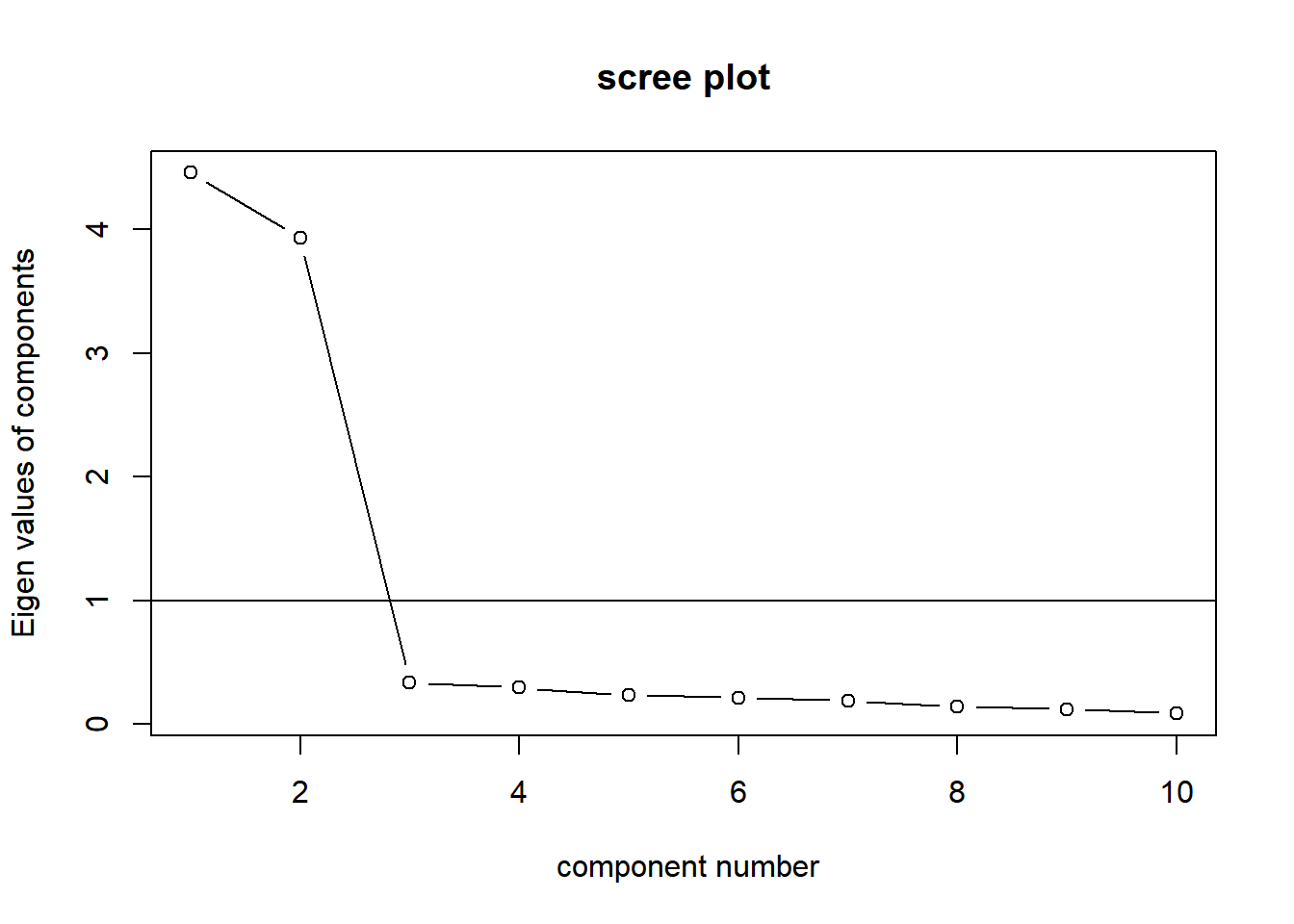

減少がなだらかになる直前までの固有値の数2を因子数として選択します。

因子負荷の推定

最尤法により因子負荷を推定します。

res_fa <- fa(r = df_data, 
             nfactors = 2,       # 因子数
             rotate = "varimax", # 回転法はvarimaxを指定
             fm = "ml"           # 最尤法を指定
             )

cor.plot(res_fa, numbers = T)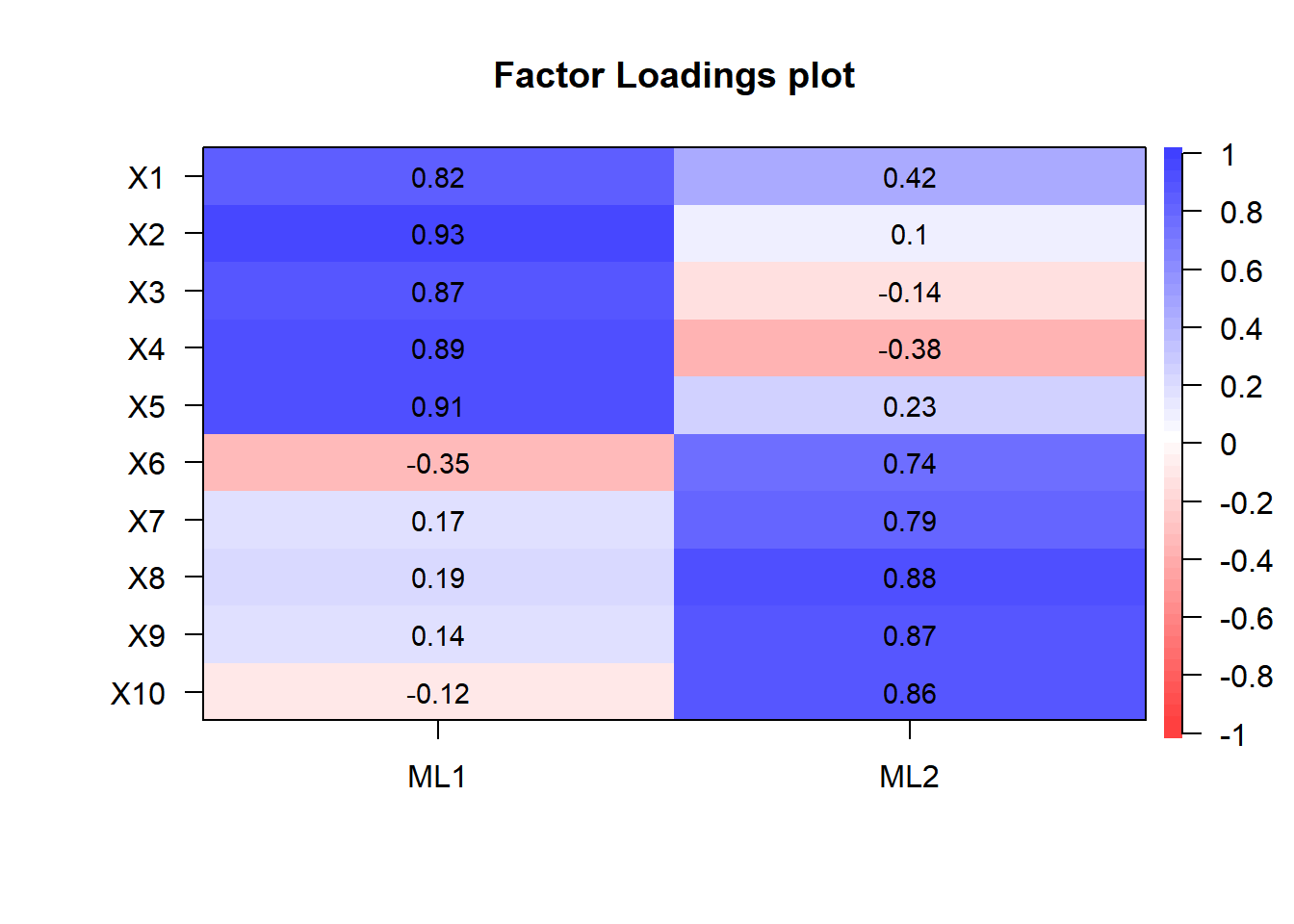

因子スコアの推定

推定した因子分析モデルから回答者ごとの因子スコア (\(f\)) を推定します。

fsc <- factor.scores(df_data, f = res_fa, 
                     method = "Harman")

df_sc <- data.frame(fsc$scores)
names(df_sc) <- c("factor.1","factor.2")

GMMのフィッティング

BICにより，コンポーネント数を選択します。

BIC <- mclustBIC(df_sc, 
                 G = 1:15, # 候補となるコンポーネント数
                 modelNames = "VVI"
                 )
plot(BIC)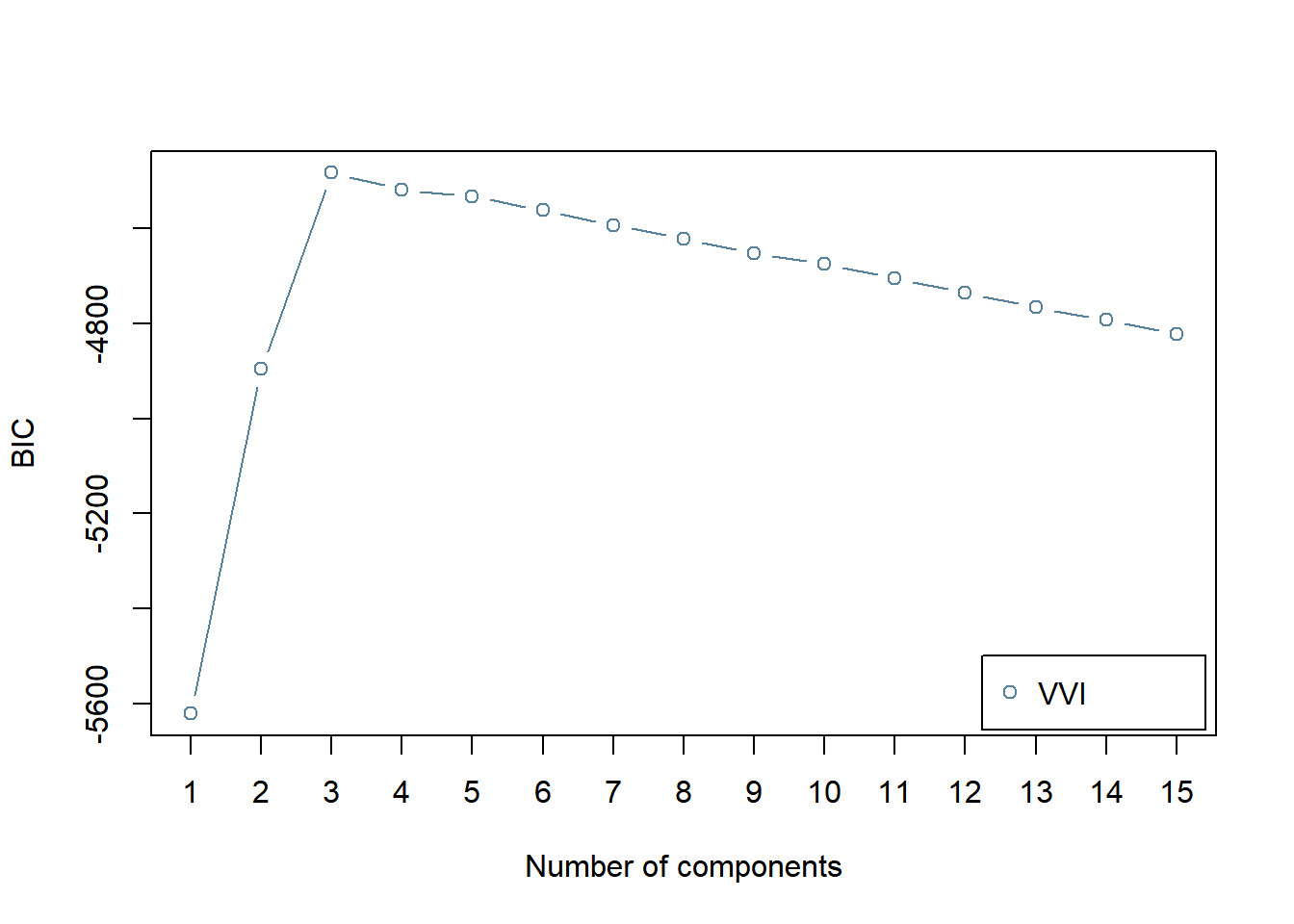

コンポーネント数として，BICの値を最大とする (MClustの仕様ではBICが大きい方が良いモデル) ， 3が選択されます。

BICで選択されたモデルの各コンポーネントの平均を求めます。

mod.GMM <- Mclust(df_sc, x = BIC)

component.centers <- t(mod.GMM$parameters$mean)

ヌルモデルとの比較による評価

各コンポーネントの平均の座標の密度と，その座標におけるヌルモデルの密度を比較し，meaningful clusterであるか否か判定します。

res_ec <- eval_component(df_sc, component.centers, 
                         n.shuffle = 100) 
## Bandwidth selection...
## kernel dinsity estimation for original data...
## kernel dinsity estimation for shuffled data...
## ==========
print(res_ec)
## $d.original
## [1] 0.3083011 0.1950971 0.2258706
## 
## $d.null
## [1] 0.1247994 0.1345762 0.1339343
## 
## $p.value
## [1] 0 0 0
## 
## $enrichment
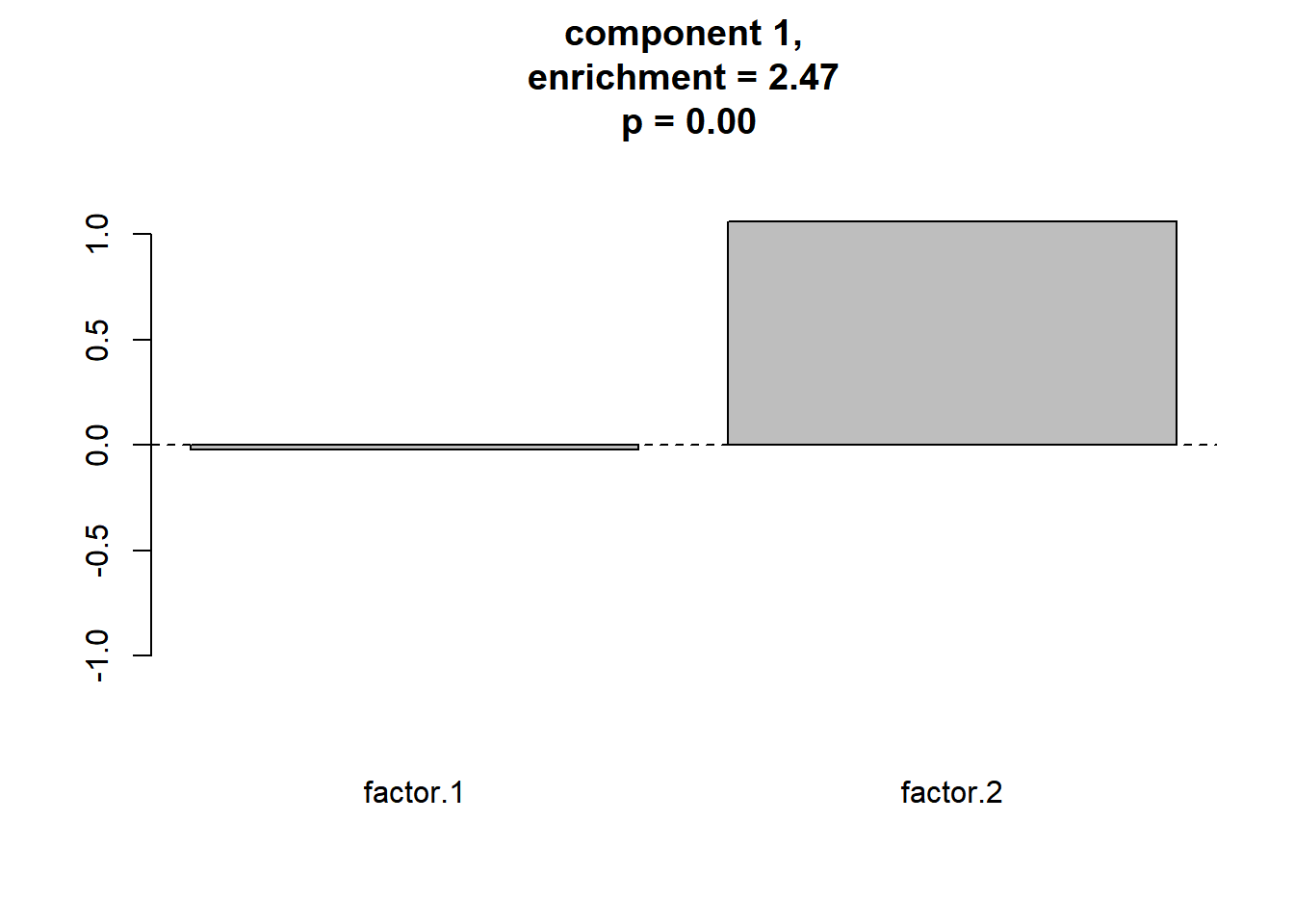
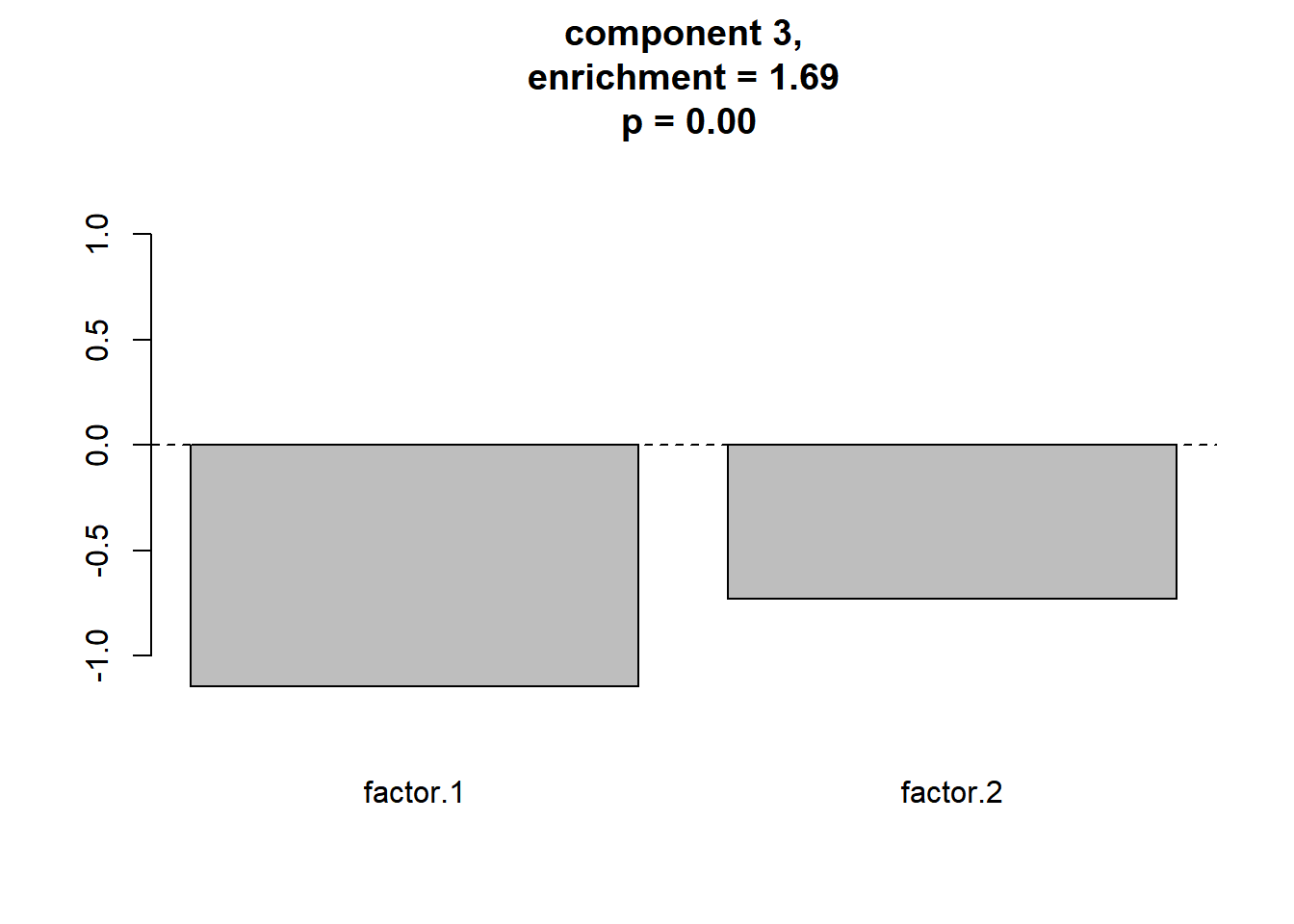
## [1] 2.470372 1.449716 1.686428

meaningful clusterをプロットします。

plot_meaningful_cluster(res_ec, # 関数eval_componentの出力
                        as.matrix(component.centers), 
                        p.threshold = 0.01, 
                        enrichment.threshold = 1.25
                        )