選択履歴・報酬履歴を説明変数としたロジスティック回帰
ここでは本書第7章で紹介したロジスティック回帰モデルを用いた簡単な解析の流れを記します。
はじめにパイプ処理などに必要になるtidyverseを呼び出します。
library(tidyverse)次にロジスティック回帰モデルに何試行前までの選択・報酬を説明変数に入れるかを設定します。
# ロジスティック回帰モデルの設定をする
rlag <- 1:5 # 説明変数に入れる報酬のラグ (1試行前,2試行前,..., 5試行前)
clag <- 1:5 # 説明変数に入れる選択のラグ (同上)もとのデータフレームに列を追加し,1試行前の選択はc1, 2試行前の選択はc2,… 1試行前の報酬はr1,…として 情報を追加すると,glmなどで回帰分析しやすくなります。また,そのためにはdplyrの関数lag()が便利です。ここではオリジナルのデータフレーム,上で定義したrlag, clagを引数とした関数を定義しておきます。ここで,データフレームは変数choiceが選択 (1 or 2)を,rewardが報酬 (0 or 1)を表すものとします。
# 与えられたデータフレームにlagをつけた説明変数を追加する関数の定義
add_lag <- function(df, rlag, clag){
# 目的変数c0は選択肢1を選んだら1, 選択肢2を選んだら0とする
df$c0 <- if_else(df$choice == 1, 1, 0)
# 選択の履歴をラグをつけて入れる
# m試行前で選択肢1を選んでいたらcm = 1, 選択肢2を選んでいたらcm = -1とする。
for (m in clag) {
df <- df %>%
mutate(tmp = if_else(lag(choice, n = clag[m]) == 1, 1, -1))
colnames(df)[ncol(df)] <- paste0("c",m) # tmpとしていた変数名をc1, c2,.. に変更
}
# 報酬の履歴をラグをつけて入れる
# m試行前で報酬が無かったらrm = 0,
# 報酬が得られ選択肢1を選んでいたらrm = 1,
# 報酬が得られ選択肢2を選んでいたらrm = -1とする。
for (m in rlag) {
df <- df %>% mutate(tmp = if_else(lag(reward, n = rlag[m]) == 1,
if_else(lag(choice, n = rlag[m]) == 1, 1, -1),
0))
colnames(df)[ncol(df)] <- paste0("r",m)
}
return(df)
}ここでは,第5章のコードgenerate_group_data_fqlearning.Rで作ったデータを読み込みます。ご自分で試される際は,ファイルのパスを適当なものに書き換えてください。
# データファイルの読み込み
dfraw <- dplyr::tbl_df(read.table("./chapter5/data/simulation_dataFQlearning_group.csv",
header = T, sep = ","))
# 必要な列だけ残す
dfs <- dfraw %>%
select(subject, trial, choice, reward)
print(dfs) ## # A tibble: 2,000 x 4
## subject trial choice reward
## <int> <int> <int> <int>
## 1 1 1 2 0
## 2 1 2 2 0
## 3 1 3 2 0
## 4 1 4 1 1
## 5 1 5 1 1
## 6 1 6 1 0
## 7 1 7 1 1
## 8 1 8 1 1
## 9 1 9 1 1
## 10 1 10 1 1
## # ... with 1,990 more rows以下で,ラグデータをsubjectごとに追加したデータフレームdflagを作成します。
# subjectごとに上で定義したadd_lagを呼び出してlagを説明変数に追加
dflag <- dfs %>%
group_by(subject) %>%
do(add_lag(., rlag, clag))
print(dflag)## # A tibble: 2,000 x 15
## # Groups: subject [10]
## subject trial choice reward c0 c1 c2 c3 c4 c5 r1
## <int> <int> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 1 2 0 0 NA NA NA NA NA NA
## 2 1 2 2 0 0 -1 NA NA NA NA 0
## 3 1 3 2 0 0 -1 -1 NA NA NA 0
## 4 1 4 1 1 1 -1 -1 -1 NA NA 0
## 5 1 5 1 1 1 1 -1 -1 -1 NA 1
## 6 1 6 1 0 1 1 1 -1 -1 -1 1
## 7 1 7 1 1 1 1 1 1 -1 -1 0
## 8 1 8 1 1 1 1 1 1 1 -1 1
## 9 1 9 1 1 1 1 1 1 1 1 1
## 10 1 10 1 1 1 1 1 1 1 1 1
## r2 r3 r4 r5
## <dbl> <dbl> <dbl> <dbl>
## 1 NA NA NA NA
## 2 NA NA NA NA
## 3 0 NA NA NA
## 4 0 0 NA NA
## 5 0 0 0 NA
## 6 1 0 0 0
## 7 1 1 0 0
## 8 0 1 1 0
## 9 1 0 1 1
## 10 1 1 0 1
## # ... with 1,990 more rows以下でGLMの回帰式を作り,全参加者を通して共通の回帰係数を推定する固定効果モデルでロジスティック回帰を行います。
# glmの回帰式を作る
fmla <- as.formula(paste("c0 ~ ",
paste(paste0("c",clag), collapse= " + "), " + ",
paste(paste0("r",rlag), collapse= " + ")))
# ロジスティック回帰 (係数は全て固定効果,すなわち全subjectで共通とする)
fit <- glm(fmla,
data = dflag %>% na.omit(), # NAを含む最初の方の試行は除外
family=binomial())この結果,モデルの式fmlaは以下のようになります。
## c0 ~ c1 + c2 + c3 + c4 + c5 + r1 + r2 + r3 + r4 + r5右辺の説明変数にはこれに加え,定数項,すなわち切片(Intercept)が自動的に入ります。切片を抜くときはモデル式に“-1”を入れる必要があります。
このように全ての説明変数を書かなくとも,データフレームを説明変数,目的変数の列だけにすれば
fit <- glm(c0 ~ . , # ドット(.)で,c0以外の全ての列を説明変数として指定する。切片はあり。
data = dflag %>%
ungroup() %>% # グループ変数が入ったままだとその列を除いても入れられてしまうので,外す
select(-c(1,2,3,4)) %>% # glmに使わない列は除く。
na.omit(), # NAを含む最初の方の試行は除外
family=binomial) とモデルの式を簡潔にすることも可能です。ただし,その場合は余計な列が入らないよう注意が必要です。
以下で結果を確認します。
summary(fit)##
## Call:
## glm(formula = fmla, family = binomial(), data = dflag %>% na.omit())
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.4047 -0.7471 -0.3339 0.7348 2.4145
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.01249 0.05660 -0.221 0.82540
## c1 -0.07459 0.08133 -0.917 0.35905
## c2 -0.12040 0.08476 -1.420 0.15549
## c3 0.08267 0.08528 0.969 0.33231
## c4 0.07428 0.08628 0.861 0.38924
## c5 0.04598 0.08419 0.546 0.58500
## r1 1.17599 0.11422 10.296 < 2e-16 ***
## r2 0.79048 0.11572 6.831 8.45e-12 ***
## r3 0.38556 0.11776 3.274 0.00106 **
## r4 0.28575 0.11859 2.410 0.01597 *
## r5 0.20093 0.11894 1.689 0.09116 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2703.2 on 1949 degrees of freedom
## Residual deviance: 1911.0 on 1939 degrees of freedom
## AIC: 1933
##
## Number of Fisher Scoring iterations: 4“Estimate”の列が各説明変数の回帰係数の推定値を表します。報酬の履歴の効果が有意であり,1試行前 (r1) がその効果は最も強く (1.17599) そこから過去にさかのぼるにつれて報酬の影響も弱くなっていくというパターンが見られます。 以下で回帰係数を棒グラフでプロットします。
g <- ggplot(data = data.frame(
regressor = names(fit$coefficients),
coefficients = fit$coefficients),
aes(x = regressor, y = coefficients)) +
geom_bar(stat = "identity")
print(g)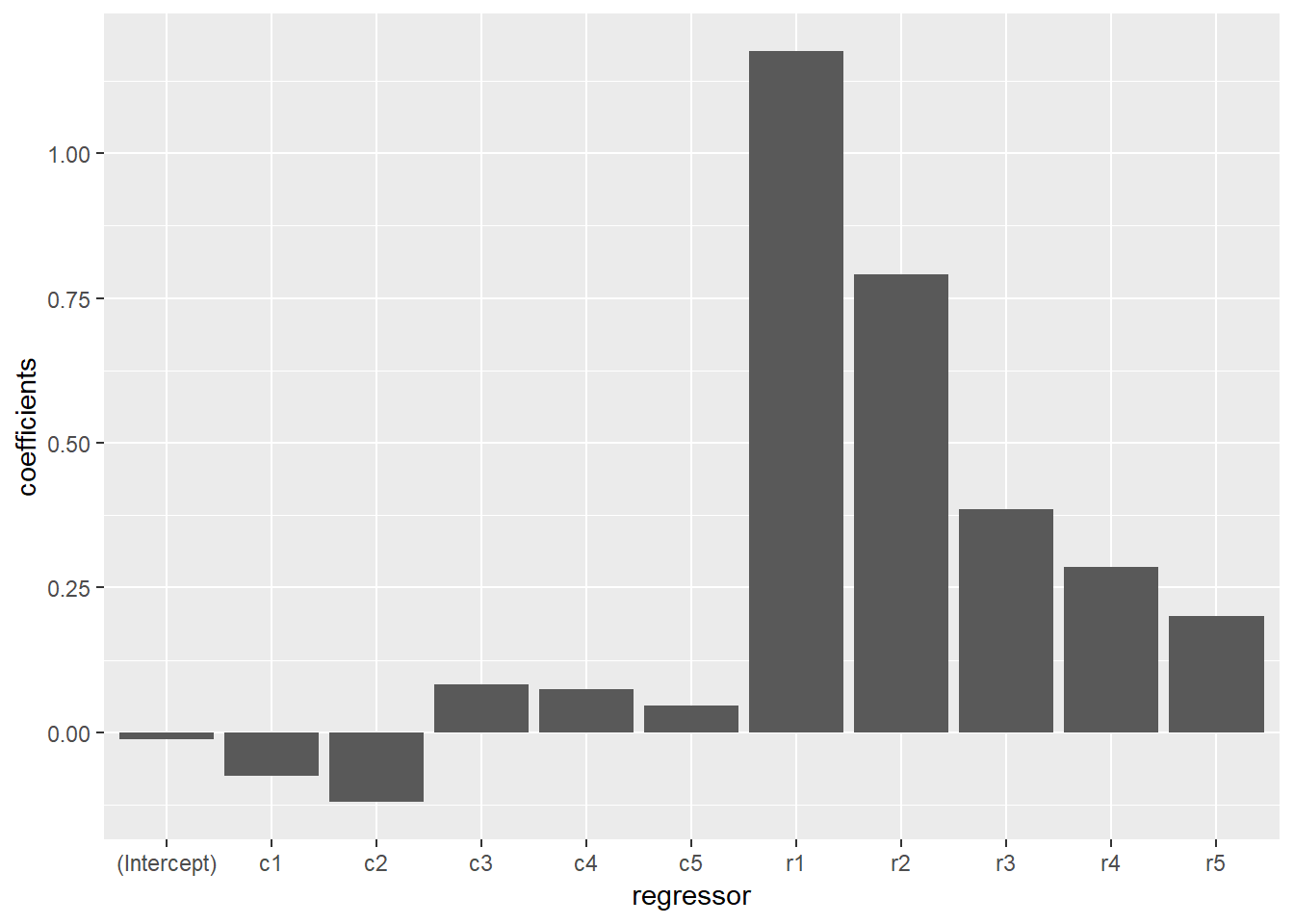
回帰係数をランダム効果とした分析などについては,改めて記したいと思います。