ここでは，実データ (Johnson-300) の解析1で Johnson-300データから出した因子スコアに対し， GMM，ヌルモデルとの比較まで行います。 実データ (Johnson-300) の解析2 からの変更点は，Gerlachrらと同様に，GMMの推定にPythonのscikit-learnパッケージを用いるところです。 scikit-learnのGMMがMClustと違うのは，初期値にK-means法の 結果を用いることができる点です。MClustは階層クラスター分析の結果を初期値に使います。今回のように，明確なクラスター構造がないデータに GMMを適用する場合は，クラスター間の距離が大きくなるよう クラスターを割り当てるK-means法の結果を初期値に使った方が 尤度を高くする解に到達しやすいようです。 RでGMMのフィッティングを実行するスクリプトを書くことは簡単ですし，他にもGMMのRのパッケージは存在するのですが，scikit-learnはそれより高速です。データサイズが大きい場合はその計算時間の差はクリティカルになってきます。

準備

以下の記事などを参考に，RからPythonを使う準備をします。
-　[@yamano357さんのブログ:reticulateパッケージでRからPythonを使う](https://qiita.com/yamano357/items/9319d4b073d82a261ed8)
Pythonがインストールされていない場合は，scikit-learnが入っているPythonのディストリビューション， Anacondaをインストールすると良いと思います。

それから，以下のコマンドをコンソールに入力してreticulateパッケージをインスト―ルしてください。

install.packages("reticulate")

パッケージや関数の読み込み

必要なパッケージを読み込みます。

library(reticulate)

こちらのページで解説した クラスター評価のための関数を読み出します。

source("functions_component_evaluation.R")

このファイルはこちらからもダウンロードできます。

データの読み込み

実データ (Johnson-300) の解析1で作成した 因子スコアデータを読み出します。パスはご自身のものに合わせてください。

df_sc <- read.csv("C:/data/personality/fs_IPIP300.csv", header = TRUE)

このcsvファイルはこちらからもダウンロードできます。

GMMのフィッティング

GMMのフィッティングを行い， BICによりコンポーネント数を選択します。

sk <- reticulate::import(module = "sklearn")
sk_gmm <- sk$mixture$GaussianMixture

klist <- 1:15 # コンポーネント数 (Gerlachは30までにしている)。
n.rep <- 20 # 異なる初期値からの繰り返し数 (Gerlachは100回にしている)

# 以下，結果を格納するための配列，リスト
biclog <- numeric(length(klist))
gmm_list <- list()
c.center_list <- list()

for (idxk in seq_along(klist)){
  K <- klist[idxk]
  likelihood <- -Inf
  
  # GMMを定義
  # scikit-learnに渡すときは整数型にする必要がある
  gmm <- sk_gmm(as.integer(K), 
                n_init = 1L,
                max_iter = 100L, 
                init_params = "kmeans") 
  
  for (idxrun in 1:n.rep) {
    
    # フィッティング
    gmm$fit(df_sc)
    
    # 対数尤度
    ll <- gmm$lower_bound_
    
    # 対数尤度がこれまでのものよりよかった場合，結果を記録
    if (ll >likelihood) {
      likelihood <- ll
      c.center_list[[idxk]] <- data.frame(gmm$means_)
      names(c.center_list[[idxk]]) <- names(df_sc)
      biclog[idxk] <- gmm$bic(df_sc)
      gmm_list[[idxk]] <- gmm
    }
  }
  cat("scikit GMM ", "K= ", K," ll= ",likelihood, "bic=", biclog[idxk], 
      "itr:", gmm$n_iter_, "\n")
}
## scikit GMM  K=  1  ll=  -6.99302 bic= 2033640 itr: 2 
## scikit GMM  K=  2  ll=  -6.936132 bic= 2017183 itr: 16 
## scikit GMM  K=  3  ll=  -6.926286 bic= 2014550 itr: 9 
## scikit GMM  K=  4  ll=  -6.922153 bic= 2013637 itr: 10 
## scikit GMM  K=  5  ll=  -6.917914 bic= 2012595 itr: 8 
## scikit GMM  K=  6  ll=  -6.912232 bic= 2011216 itr: 9 
## scikit GMM  K=  7  ll=  -6.912157 bic= 2011447 itr: 9 
## scikit GMM  K=  8  ll=  -6.909569 bic= 2010937 itr: 9 
## scikit GMM  K=  9  ll=  -6.907062 bic= 2010444 itr: 8 
## scikit GMM  K=  10  ll=  -6.905558 bic= 2010253 itr: 8 
## scikit GMM  K=  11  ll=  -6.904436 bic= 2010202 itr: 8 
## scikit GMM  K=  12  ll=  -6.903364 bic= 2010148 itr: 9 
## scikit GMM  K=  13  ll=  -6.902402 bic= 2010116 itr: 9 
## scikit GMM  K=  14  ll=  -6.901097 bic= 2009982 itr: 9 
## scikit GMM  K=  15  ll=  -6.900168 bic= 2009960 itr: 9
plot(klist, biclog, type = "l", 
     xlab = "Number of components", ylab = "BIC")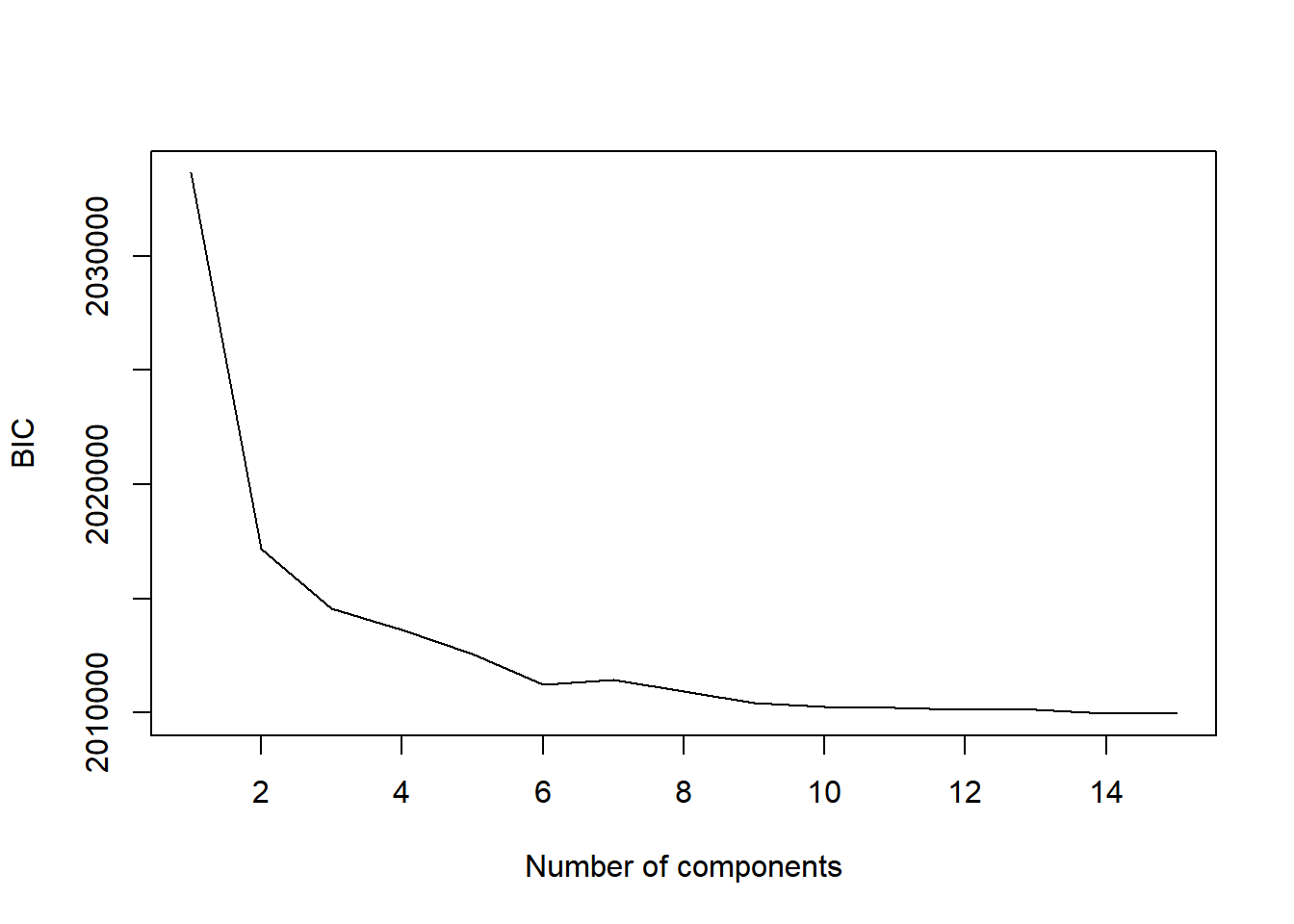

Gerlachらは単にBICが最小になったところを選ぶのではなく， ブートストラップ法を使った検定を行い，BICが有意に減少しなく なるコンポーネント数として，13を選択しています。 ここでは，そこまではしませんが， Gerlachらにならって，コンポーネント数は13を選択します。

BICで選択されたモデルの各コンポーネントの平均を求めます。

idxk <- which(klist == 13)
component.centers <- c.center_list[[idxk]]

ヌルモデルとの比較による評価

各コンポーネントの平均の座標の密度と，その座標におけるヌルモデルの密度を比較し，meaningful clusterであるか否か判定します。

なお，シャッフルの回数はGerlachらは1000回にしていますが， ここでは時間の短縮のため20回のみにしました。

res_ec <- eval_component(df_sc, component.centers, 
                         n.shuffle = 20) 
## Bandwidth selection...
## kernel dinsity estimation for original data...
## kernel dinsity estimation for shuffled data...
## ==
print(res_ec)
## $d.original
##           1           2           3           4           5           6 
## 0.005526820 0.007386424 0.001002944 0.002816708 0.010009359 0.003370110 
##           7           8           9          10          11          12 
## 0.002814864 0.004757709 0.002858488 0.009235408 0.002469255 0.006150435 
##          13 
## 0.002957968 
## 
## $d.null
##  [1] 0.005442782 0.005099011 0.001118303 0.003086953 0.006217502
##  [6] 0.004017524 0.003138894 0.004482056 0.002685799 0.006382228
## [11] 0.002987596 0.004027899 0.003220678
## 
## $p.value
##  [1] 0.35 0.00 0.90 0.95 0.00 1.00 1.00 0.05 0.20 0.00 1.00 0.00 0.90
## 
## $enrichment
##  [1] 1.0154402 1.4485995 0.8968446 0.9124557 1.6098682 0.8388524 0.8967692
##  [8] 1.0615014 1.0642969 1.4470507 0.8265020 1.5269587 0.9184302

meaningful clusterをプロットします。

plot_meaningful_cluster(res_ec, # 関数eval_componentの出力
                        component.centers, 
                        p.threshold = 0.01, 
                        enrichment.threshold = 1.25
                        )

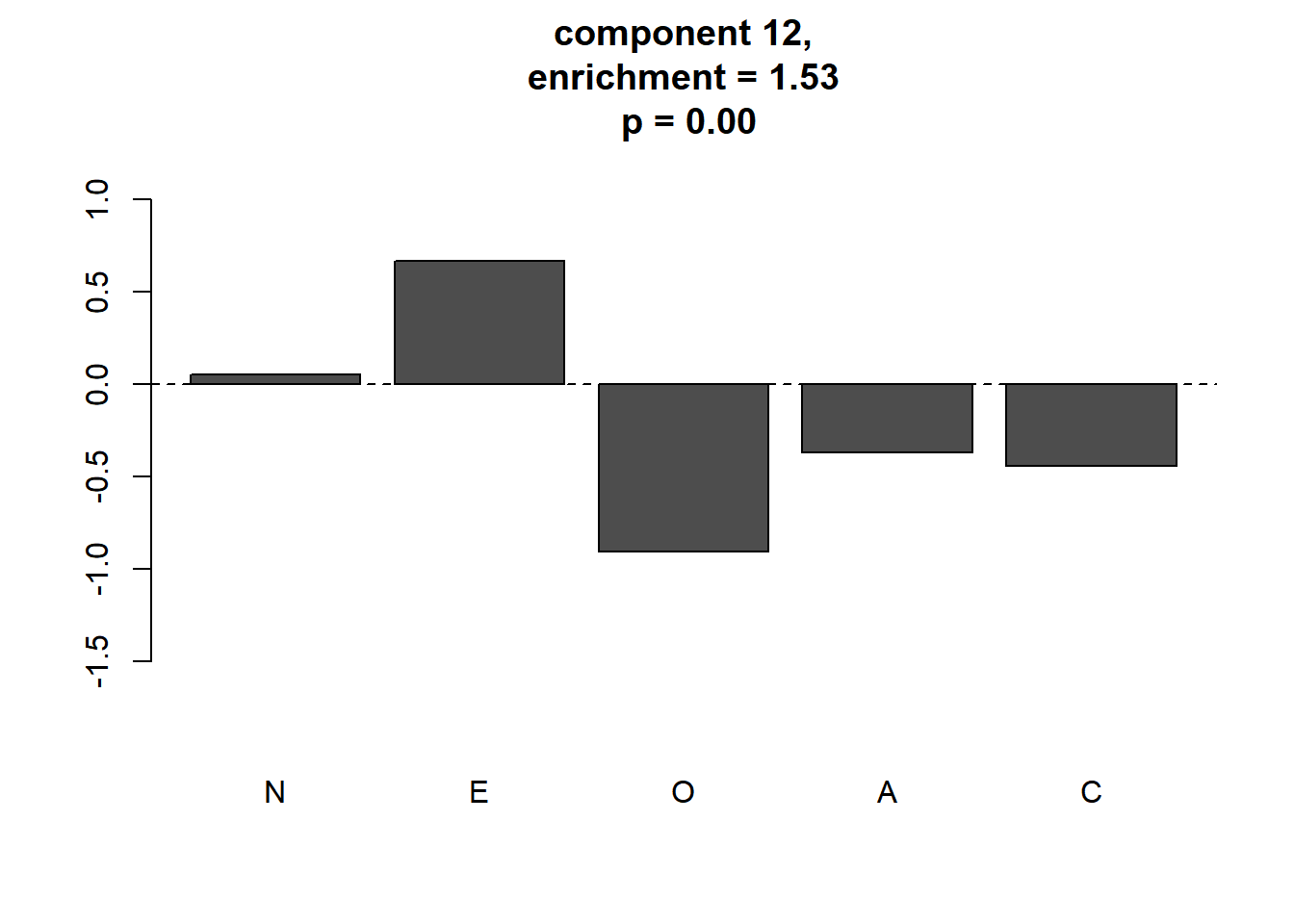
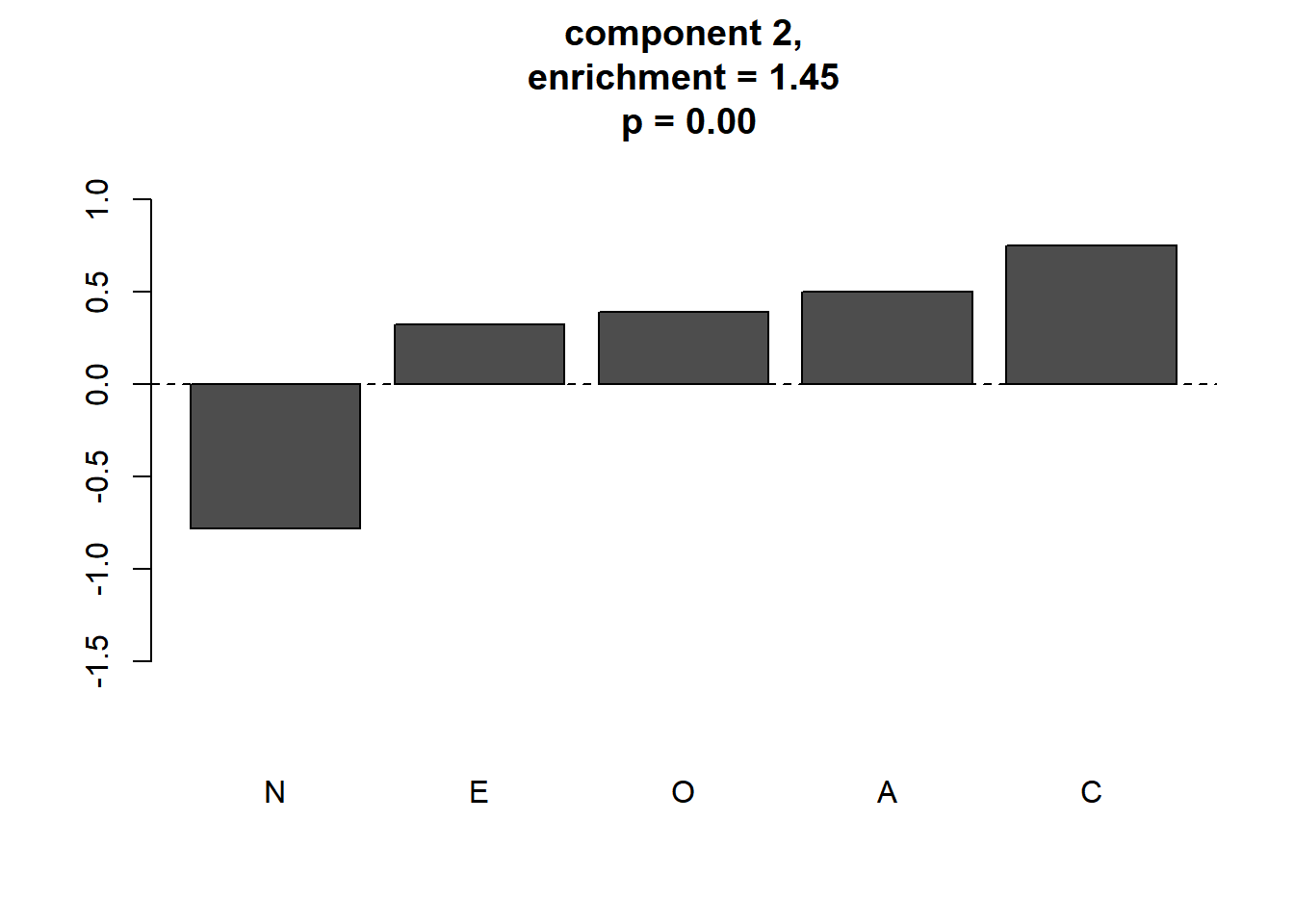
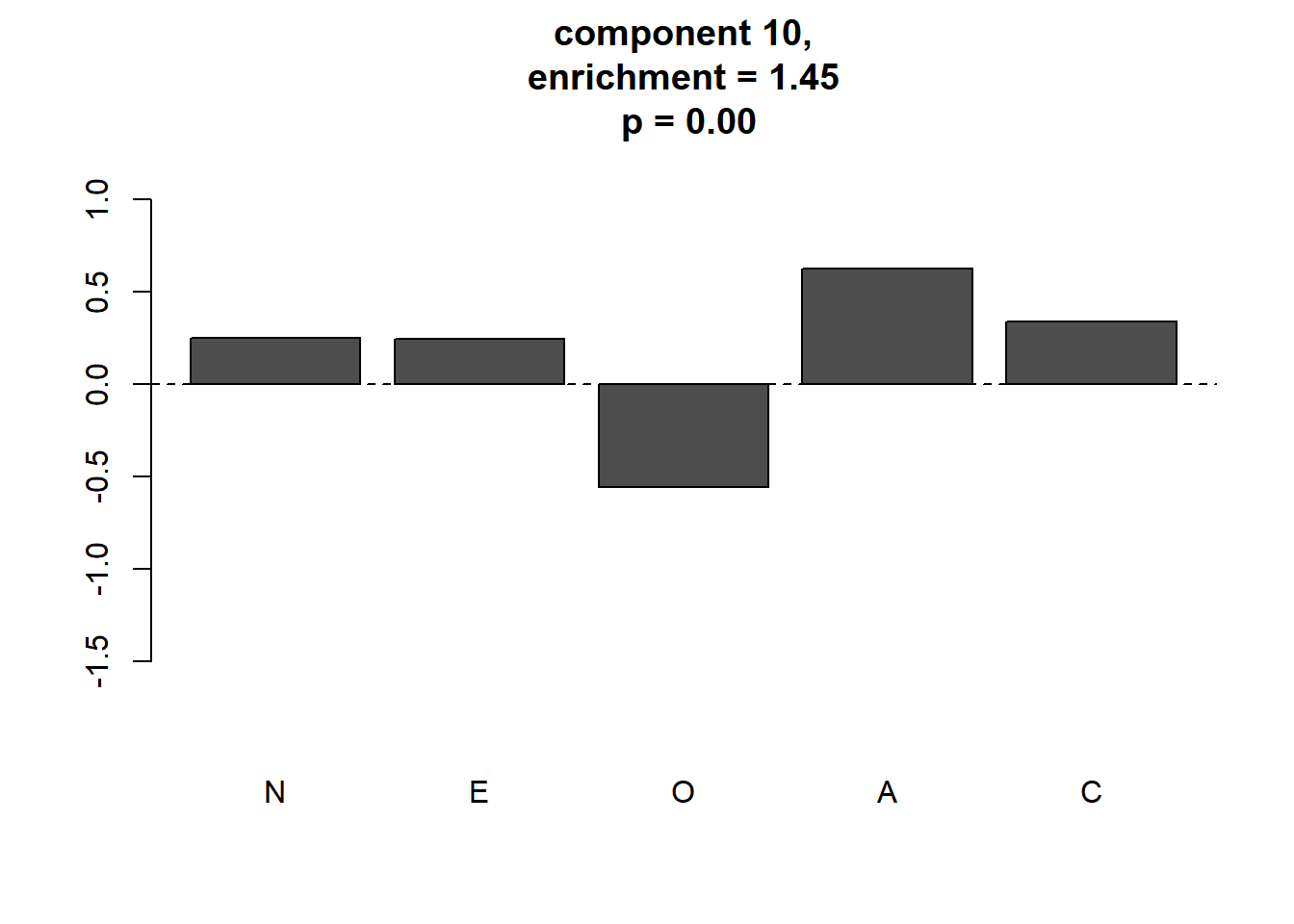4つのmeaningful clusterが同定されました。この4つがGerlachらが同定した パーソナリティの4つの“タイプ”に対応すると考えられます。 GerlachらのFig.2と見比べると，順に“Reserved”, “Self-centered”, “Role model”, “Average”に対応します。 “Average”はパターンが やや異なっていますが，このタイプは 不安定であり，ピークは明確ではないため初期値などによって 変わるようです。