回答ミス数のモデリング

IPIP-NEO-300データに関して，無回答項目数の分布のモデルを検討し， その背景にあるメカニズムについて考えてみます。

ここでは，実データ (Johnson-300) の解析: 回答ミスがある回答者の分析 で記録した無回答項目数へモデルを当てはめます。

なお，ここで扱うのは総計30万7313人分の回答ミス数という大規模なデータになっており，信頼性の高い推定が可能となります。

準備

必要なパッケージを読み込みます。

library(MASS) # 負の二項分布等の最尤推定に用いる
library(pscl) # ハードルモデル，ゼロ切断モデル用

描画のための関数設定

カウントデータのヒストグラムとフィットした分布を 重ねてプロットするための関数を定義しておきます。

# プロット用関数
plot.dist <- function(density, dist.name = "fitted distribution"){
  mp <- barplot(table(df_data$count.miss)/length(df_data$count.miss),
              xlab = "Number of missed items", 
              ylab = "Probability",
              ylim = c(0,0.6))
  lines(mp, density, type = "o", lwd = 3, col = "#332288", lty = 1)
  legend("topright",
       legend = dist.name,
       lty = 1, col = "#332288", 
       lwd = 3, 
       bty = "n")
}

データの読み込み

無回答項目数を読み込みます。

df_data <- read.csv("./data_count_miss_IPIP300.csv", header = TRUE)

# 考えるカウント数の系列 (このデータの場合，0:10)
xcount <- 0:max(df_data)

モデルのフィッティング

以下，モデルごとに最尤推定でパラメータを推定し， 実際のデータと合わせてプロットします。

ポアソン分布

ポアソン分布の確率質量関数は，\(x\)を観測されるカウント数とし， \[ \text{Poisson}(x|\lambda) = \frac{\lambda^x}{x!} e^{-\lambda} \] と表されます。パラメータ\(\lambda\)を推定します。

mod.poisson <- fitdistr(df_data$count.miss, densfun = "poisson")
plot.dist(dpois(xcount, mod.poisson$estimate), "Poisson")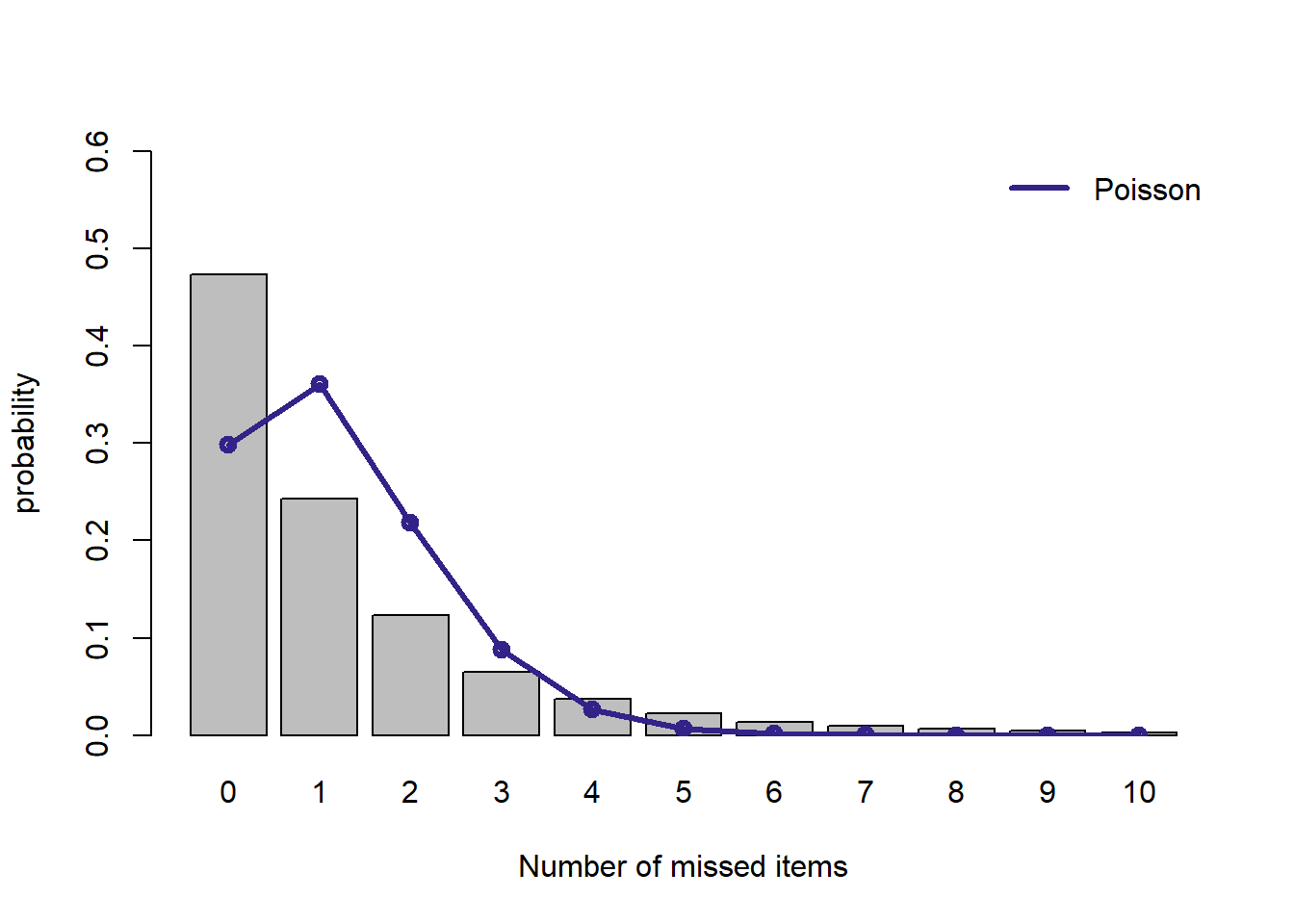

実データ (Johnson-300) の解析: 回答ミスがある回答者の分析 でも見たように，このデータの分布 (グレイのバー)にはポアソン分布 (青い実線) はフィットしません。

幾何分布

幾何分布の確率質量関数は \[ \text{Geometric}(x|p) = p (1-p)^x \] と表されます。パラメータ\(p\)を推定します。

mod.geometric <- fitdistr(df_data$count.miss, densfun="geometric")
d.geometric <- dgeom(xcount, prob = mod.geometric$estimate[1])

plot.dist(d.geometric, "Geometric")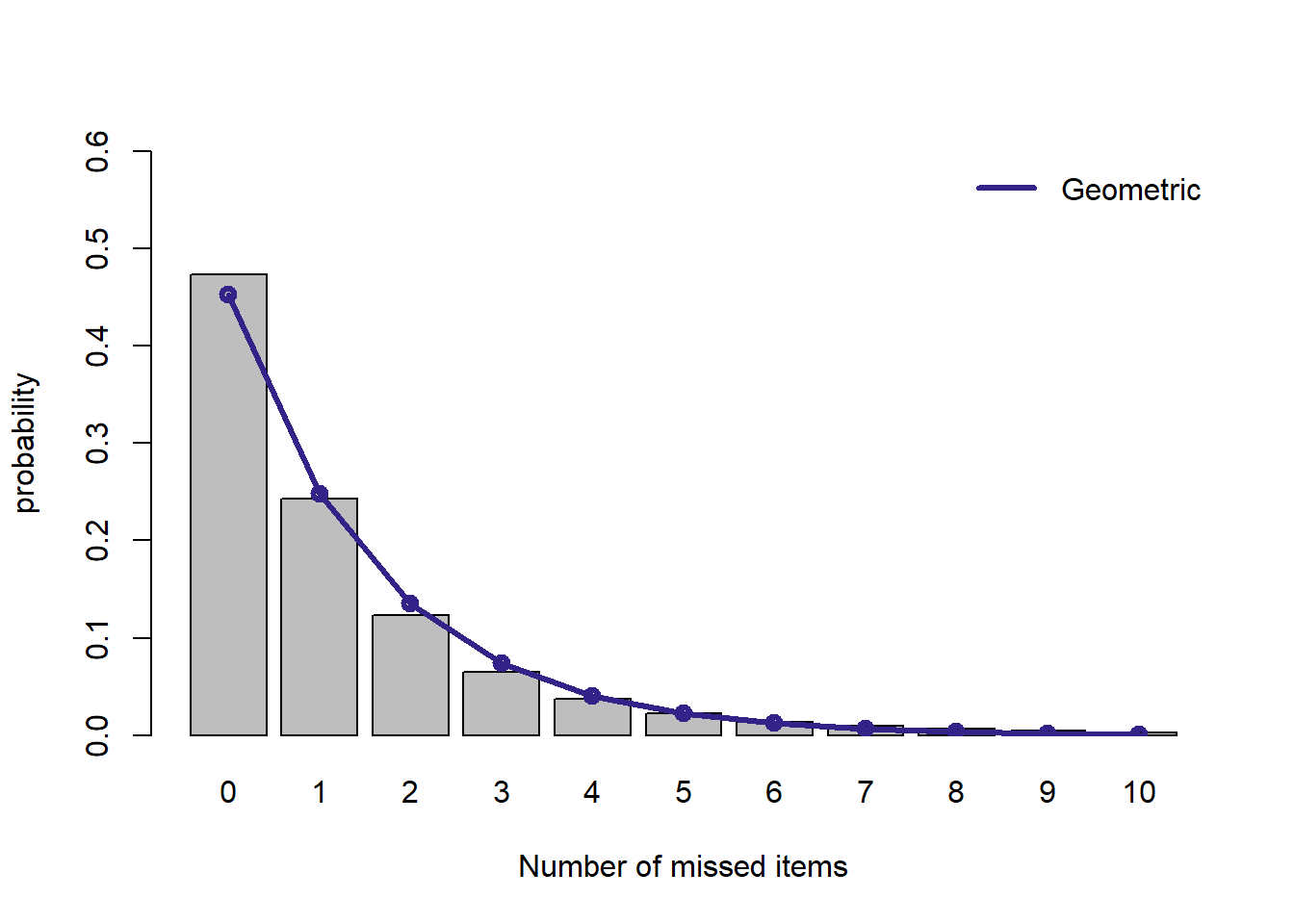

ポアソン分布に比べるとよくフィットします。 しかし，反応ミス数が0, 1のときはその確率は過小評価，2, 3のときはやや過大評価されているようです。

負の二項分布

負の二項分布の確率質量関数は \[ \text{NegBinom}(x|n, p) = \frac{\Gamma(x+n)}{\Gamma(n) x!} p^n (1-p)^x \] と表されます。ここで，\(\Gamma(x)\)はガンマ関数を表します。 \(x\)が整数の場合は\(\Gamma(x+1) = x!\)という関係があり， \(\Gamma(x+n) = (x+n-1)!\), \(\Gamma(n) = (n-1)!\)として表現されることもあります。 負の二項分布のパラメータは「サイズパラメータ」\(n\)と「成功確率」\(p\)の二つです。 MASSパッケージでは成功確率\(p\)と，\(p = \frac{n}{n + \mu}\)という関係があるパラメータ\(\mu\)が推定されます。

mod.negbin <- fitdistr(df_data$count.miss, 
                       densfun="negative binomial")

n <- mod.negbin$estimate[1]
mu <- mod.negbin$estimate[2]
p <- n / (n + mu) # 成功確率

d.nb <- dnbinom(xcount, size = n, prob = p)
plot.dist(d.nb, "Negative binomial")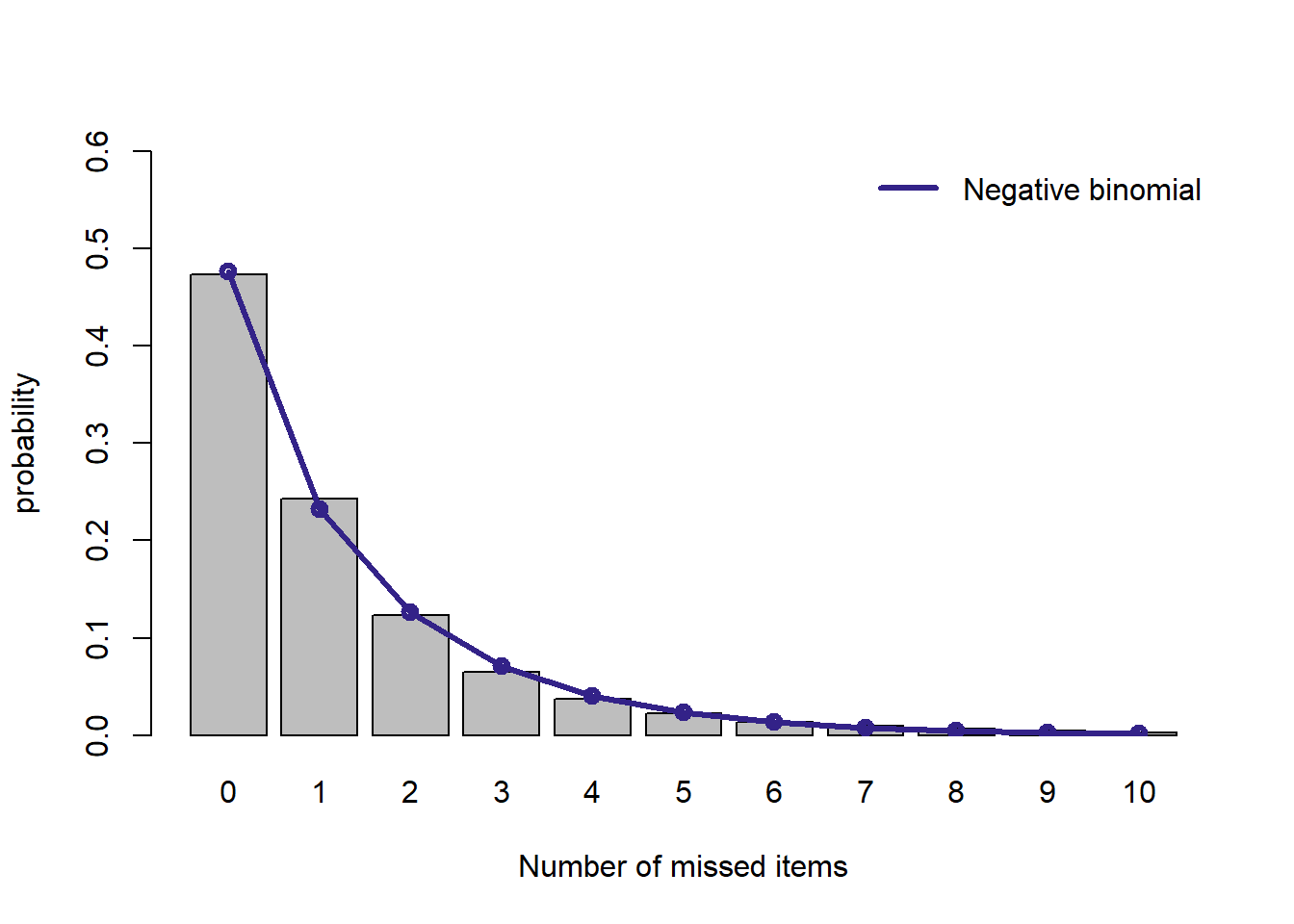

わずかにずれはありますが，幾何分布よりもよくフィットしています。

ハードルモデル (ゼロ切断ポアソン分布)

ハードルモデルについては https://qiita.com/nozma/items/52211b1bacaa8a898164 を参照してください。

簡単にいうと，ハードルモデルでは，1段階目のステップとして 回答者ごとに一定の確率に基づいて， ゼロを出す (回答ミスをしない) 回答者であるか，1つ 以上の回答ミスを出す回答者であるか決まるとします。 回答ミスをする回答者のミス数は，ゼロを含まない離散分布から生成 されます。2段階目でサンプリングする離散分布として，psclパッケージの hurdle関数のデフォルトではゼロ切断ポアソン分布が用いられます。 まずはそのゼロ切断ポアソン分布を用います。

mod.hurdle.poiss <- pscl::hurdle(count.miss ~ 1, df_data)
d.h <- predict(mod.hurdle.poiss, type = "prob")[1,]

plot.dist(d.h, "Hurdle (Poisson)")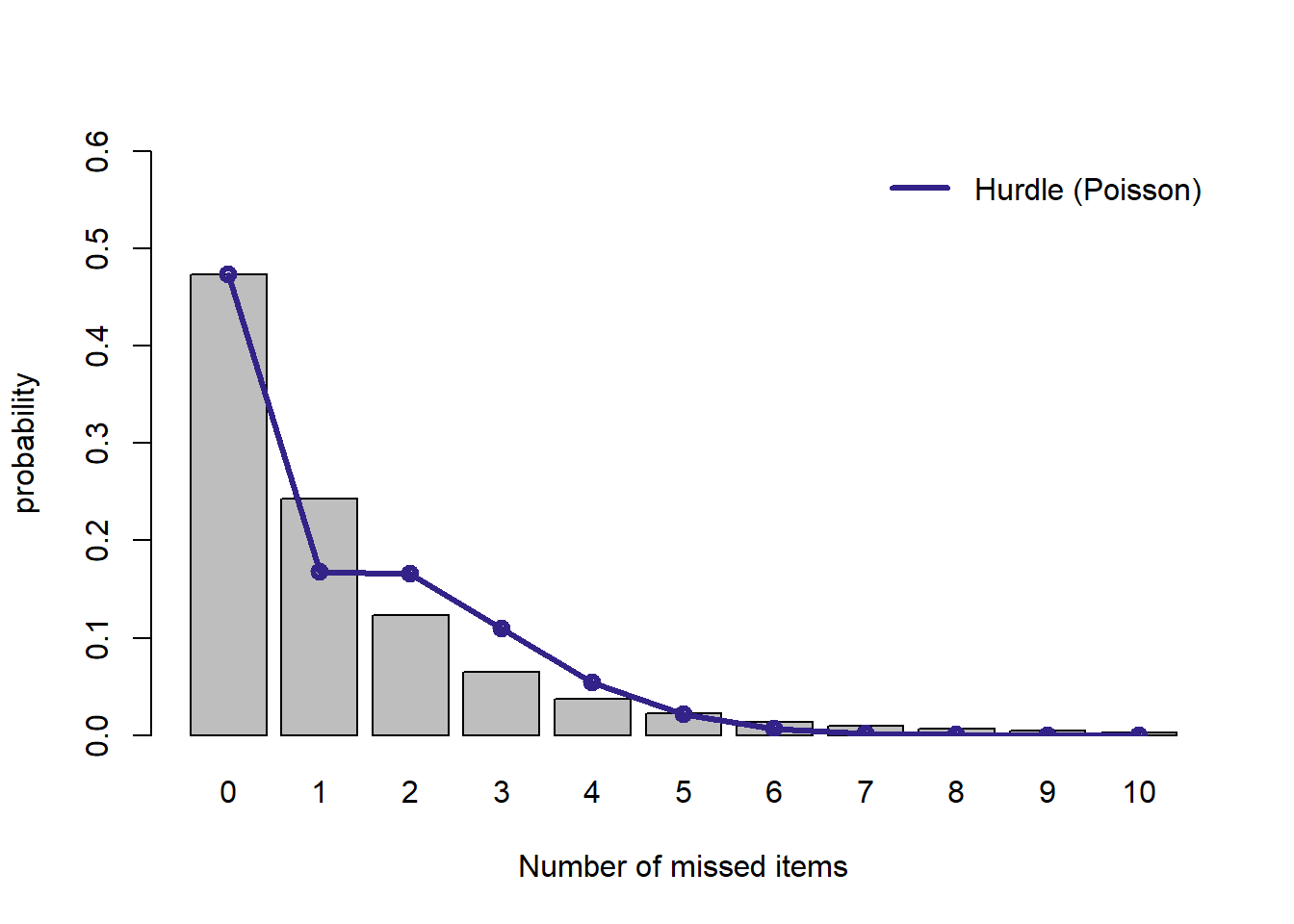

ハードルモデルの構造上，ゼロの値のカウントは完璧にフィットするのですが， それ以上の値になるとあまりよくフィットしません。 ゼロ切断ポアソン分布はこの分布に適合しないようです。

predict関数による予測の取り出しは以下のサイトを参考にしました。 https://uvastatlab.github.io/2016/06/01/getting-started-with-hurdle-models/

ハードルモデル (負の二項分布)

次に2段階目でサンプリングする離散分布として，(ゼロを含まない) 負の二項分布を用います。

mod.hurdle.nb <- hurdle(count.miss ~ 1, data = df_data, 
                        dist = "negbin")
d.h <- predict(mod.hurdle.nb, type = "prob")[1,]

plot.dist(d.h, "Hurdle (Negative binomial)")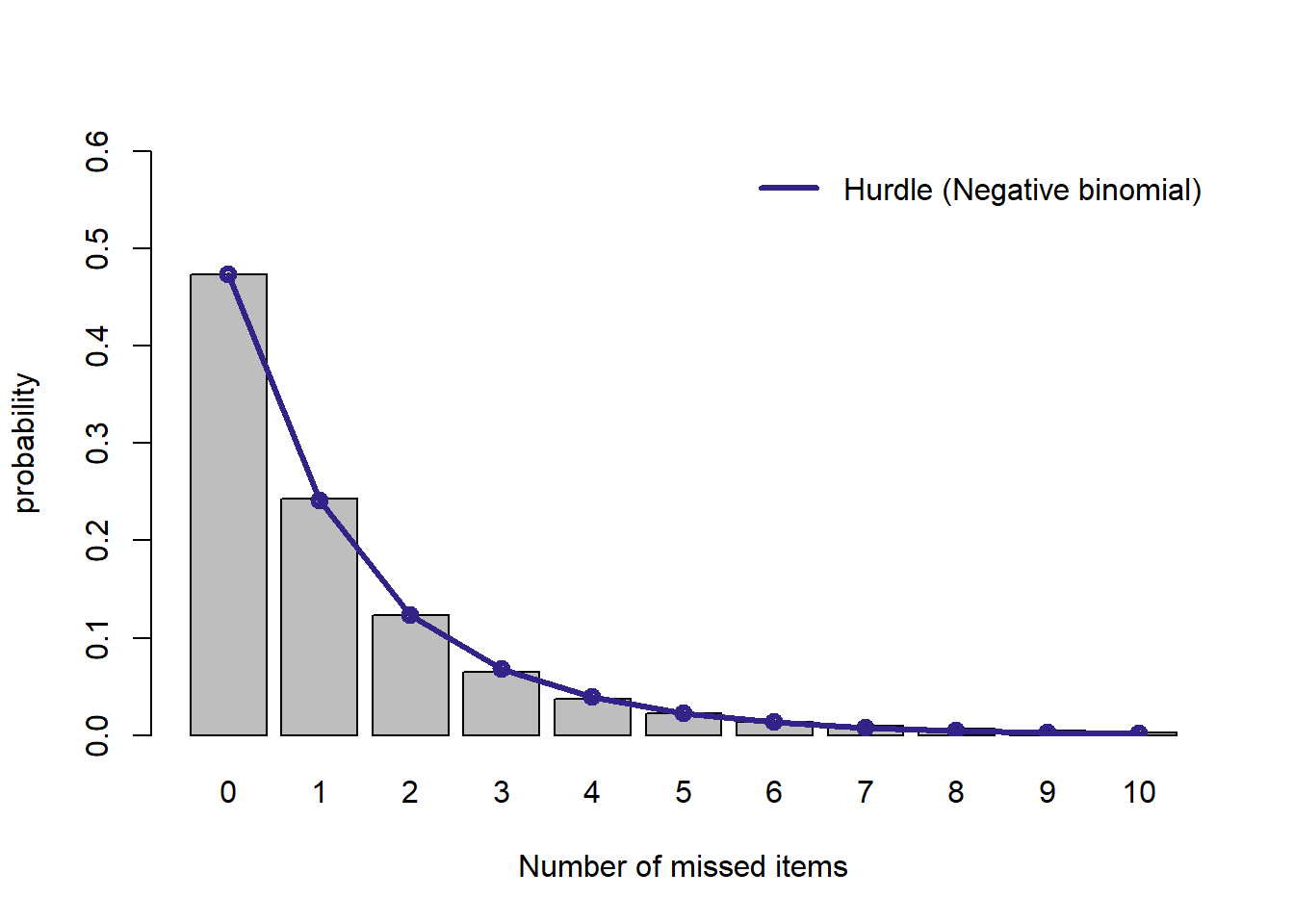

(純粋な)負の二項分布と比べても，このハードルモデルは良くフィットしているようです。

なお，このハードルモデルは (純粋な) 負の二項分布を含むため (1段階目のステップでゼロになる確率を負の二項分布でゼロをとる確率に 一致させればその負の二項分布と等価になる)， 尤度は負の二項分布に比べて同等かそれ以上になります。

ゼロ過剰モデル (ポアソン分布)

ゼロ過剰モデルでは， 第1ステップで離散分布から回答ミス数をサンプリングします。 ここでの離散分布はゼロを含んでいても構いません。 第2ステップでは一定の確率で値を0にします。 ゼロ過剰モデルについても https://qiita.com/nozma/items/52211b1bacaa8a898164 を参照してください。

離散分布として，まずはポアソン分布を用います。

mod.zeroinfl.poiss <- pscl::zeroinfl(count.miss ~ 1, df_data, 
                                     dist = "poisson")
d.zeroinfl <- predict(mod.zeroinfl.poiss, type = "prob")[1,]
plot.dist(d.zeroinfl, "Zero inflated (Poisson)")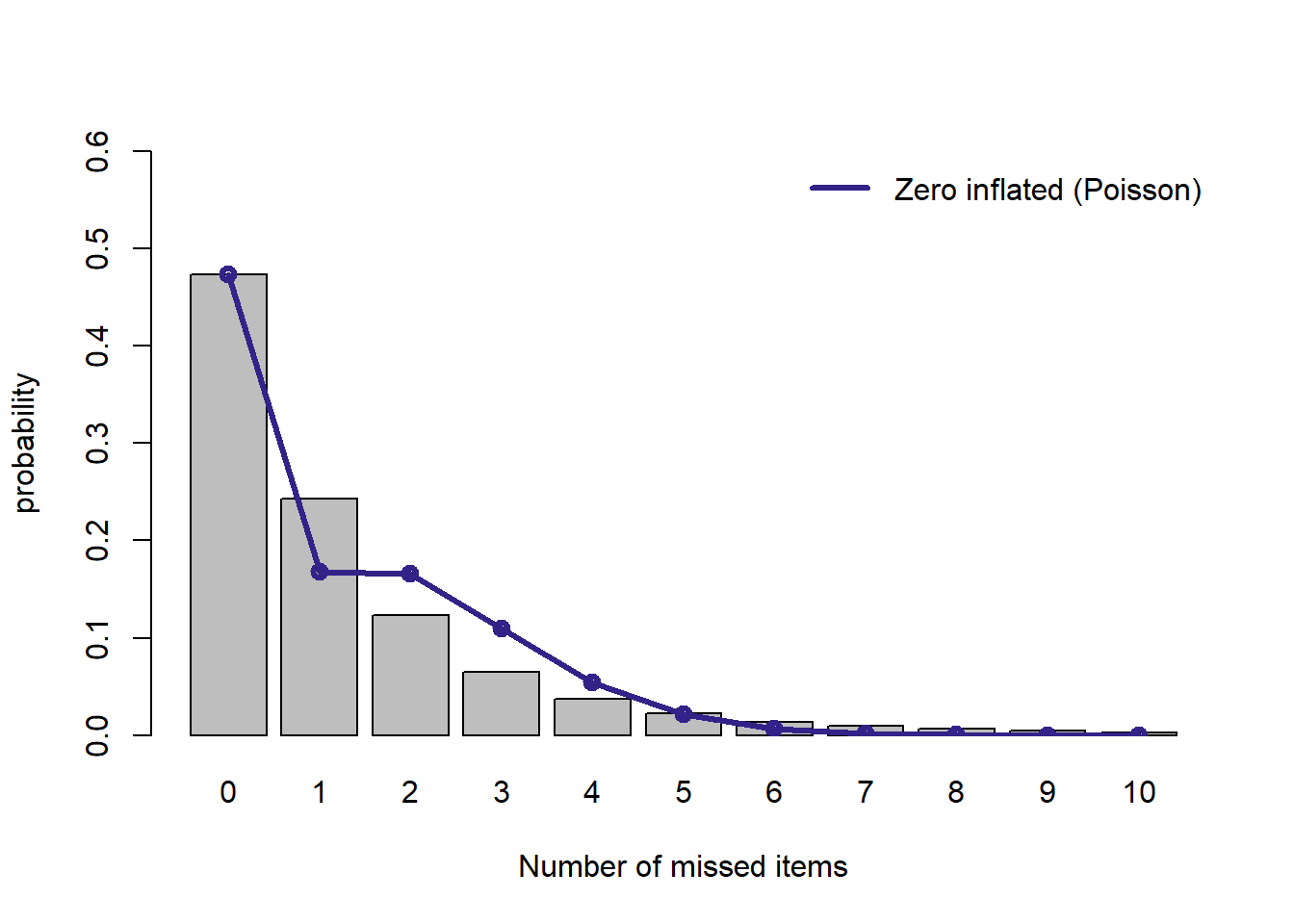

ゼロ過剰モデルも構造上，ゼロとなる数は完璧にフィットするのですが， それ以上の値になるとあまりよくフィットしません。

ゼロ過剰モデル (負の二項分布)

次に離散分布として，負の二項分布を用います。

mod.zeroinfl.nb <- pscl::zeroinfl(count.miss ~ 1, df_data, dist = "negbin")
d.zeroinfl.nb <- predict(mod.zeroinfl.nb, type = "prob")[1,]
plot.dist(d.zeroinfl.nb, "Zero inflated (negative binomial)")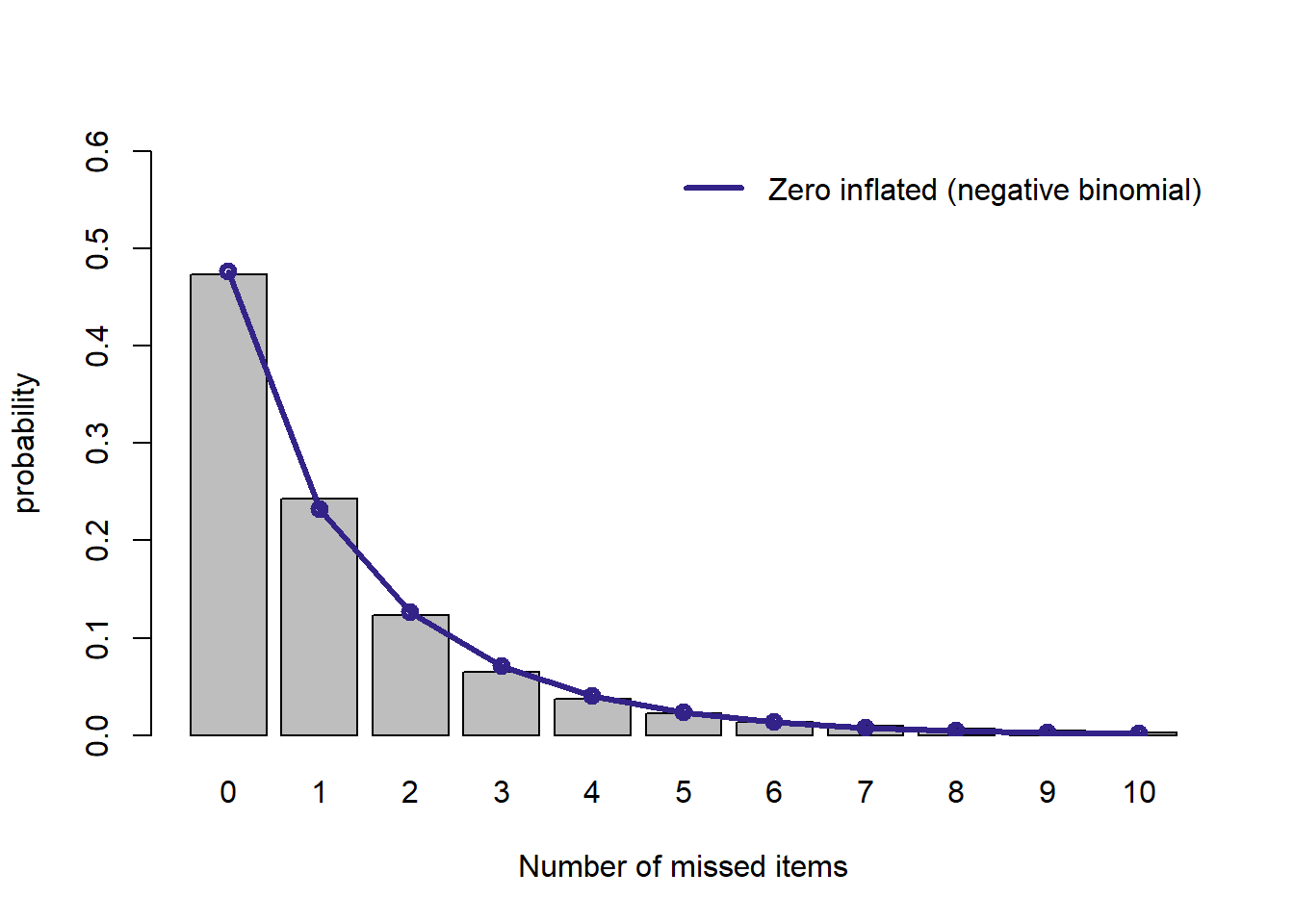

ポアソン分布を用いた場合と比べるとよくなりますが， 負の二項分布を用いたハードルモデルに比べるとフィットはよくないようです。

AIC によるモデル選択

AICを比較してみます。

AIC(mod.poisson, # ポアソン分布
    mod.geometric, # 幾何分布
    mod.negbin, # 負の二項分布
    mod.hurdle.poiss, # ハードルモデル (離散分布はポアソン分布)
    mod.hurdle.nb,  # ハードルモデル (離散分布は負の二項分布)
    mod.zeroinfl.poiss, # ゼロ過剰モデル (離散分布はポアソン分布)
    mod.zeroinfl.nb # ゼロ過剰モデル (離散分布は負の二項分布)
    ) 

	df	AIC
mod.poisson	1	1069408.5
mod.geometric	1	935048.6
mod.negbin	2	933643.9
mod.hurdle.poiss	2	977969.9
mod.hurdle.nb	3	933422.6
mod.zeroinfl.poiss	2	977969.9
mod.zeroinfl.nb	3	933646.0

負の二項分布を離散分布とするハードルモデルがAICが 最低となり，最も予測力のあるモデルと判断できます。 次いで，負の二項分布が良いようです。 ただし，ここまでサンプル数が多いと (30万人以上) パラメータ数に応じた ペナルティはほとんど働かなくなるので解釈には注意が必要です。 なお，BICでも同様の結果になります。 (BICは，上の関数AICにk = log(length(df_data$count.miss)) をオプションに入れれば計算できます。)

反応ミス率の分布の推定

負の二項分布は，それぞれの個人の回答ミス数がポアソン分布に従うと仮定し， そのポアソン分布のパラメータ\(\lambda\)が個人ごとにガンマ分布 \[ \text{Gamma}(\lambda|a,b) = \frac{b^a}{\Gamma (a)} \lambda^{a - 1} e^{-b \lambda} \] に従って決定されると仮定したときの個人の回答ミス数の分布ととらえられます (証明は付録参照)。また，幾何分布は負の二項分布で\(n = 1\)とした場合の特殊形であり，このとき対応するガンマ分布は指数分布となります。

以下に，これらの関係を図示します。

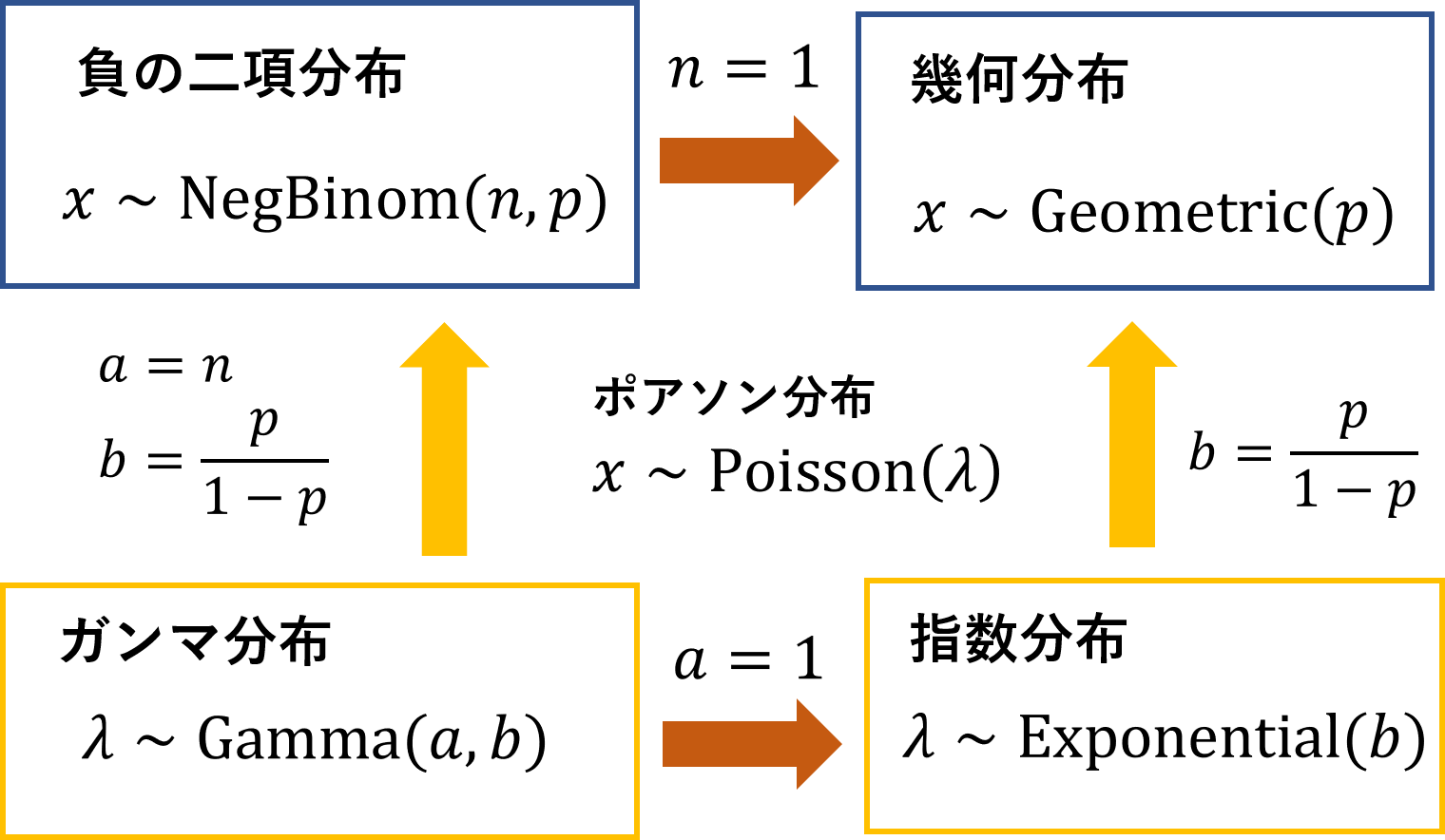
分布間の関係図

ここでは上でフィットした負の二項分布や幾何分布のパラメータから，対応する \(\lambda\)の分布をプロットしてみます。

# 色のリスト
collist <- c("#CC6677", "#44AA99")
# ラインスタイルのリスト
ltylist <- c(2,1)

x <- seq(0, 10, by=0.01)

# 幾何分布に対応する指数分布
b <- mod.geometric$estimate[1] / (1 - mod.geometric$estimate[1])
plot(x, dexp(x, rate = b), type="l", 
      col = collist[[1]], lwd = 3, 
     lty = ltylist[1], 
     xlab = "mean miss rate (per 300 items)", 
     ylab = "probability density",ylim = c(0,2))

# 負の二項分布に対応するガンマ分布
a <- mod.negbin$estimate[1]
mu <- mod.negbin$estimate[2] 
p <- a / (a + mu) # success rate

lines(x, dgamma(x, shape = a, rate = p / (1-p)), 
      lty = ltylist[2], type = "l", col = collist[[2]], lwd = 3)

legend("topright",
       legend = c("Exponential","Gamma"),
       lty = ltylist, col = collist, lwd = 3, 
       bty = "n")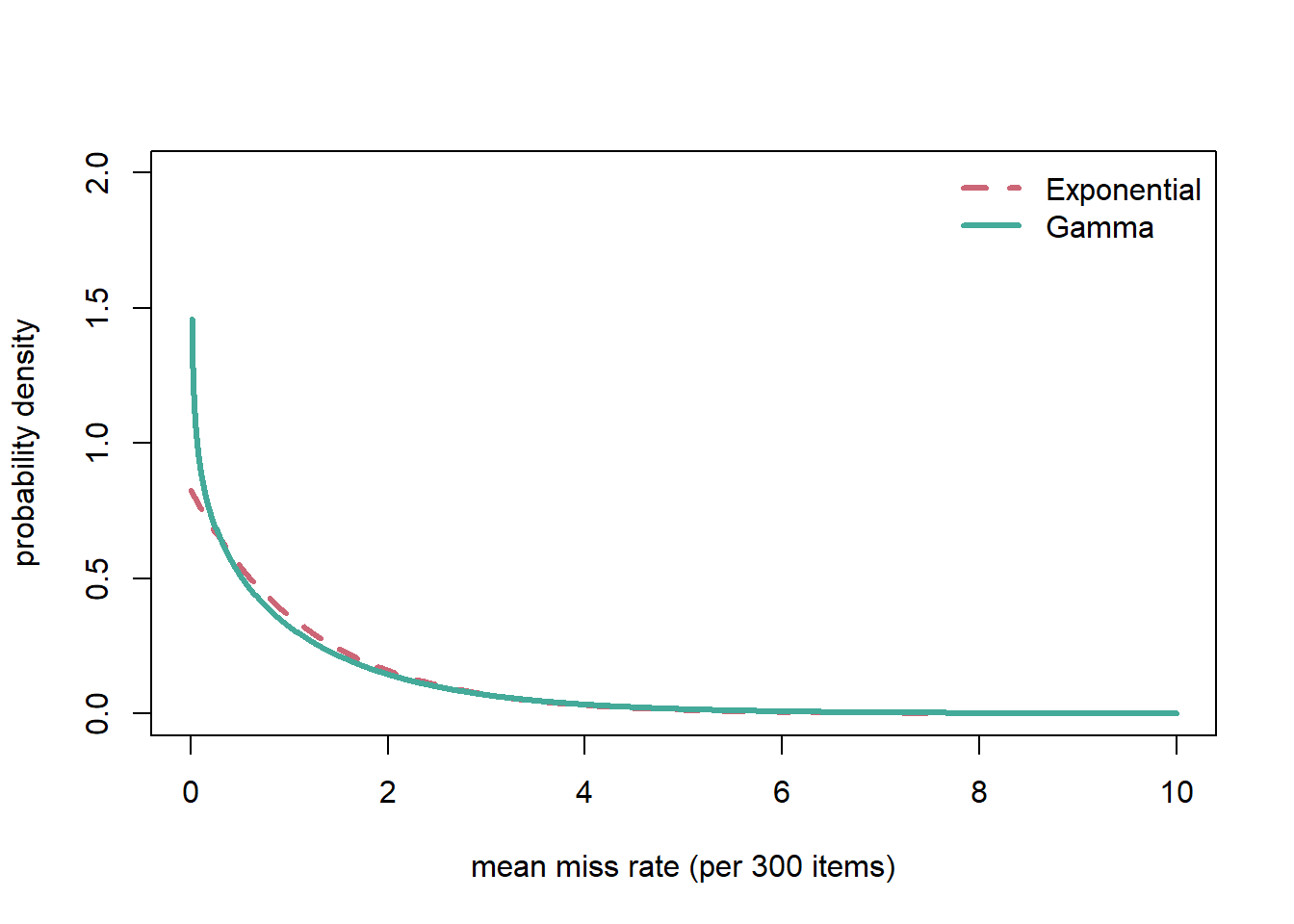

負の二項分布が幾何分布と比べてフィットがよかったことを 考えると，反応ミス率はゼロに近い回答者が多い 一方，指数関数が予測するよりはゆっくり減衰する，つまり 反応ミスが結構多い人もいる，という大きな個人差があることが 推察できます。 しかしこれは，あくまで個人の回答ミス数がポアソン分布に従うと いう前提のもとでの話です。この前提は，例えば 全回答者が一定のミス率で項目ごとに独立に反応ミスが起こる，というときに 成り立ちます。 また，後半の項目の方が疲れてミスが増える，という傾向があっても， その傾向が全回答者で全く同一であれば，やはり全体の回答ミス数は ポアソン分布に従います。これは， ポアソン分布に従う変数を足し合わせた 変数は，個々のポアソン分布のパラメータが違っていても やはりポアソン分布に従うという性質があるためです。

一方で，もし回答ミスの頻度に個人内で自己相関があれば (例えば一度ミスをするとまたすぐミスしやすいというような)， 一人一人の回答ミス数もポアソン分布には従わなくなります。 興味のある方はシミュレーションなどで検討してみてください。

付録

ここでは，負の二項分布や幾何分布が，それぞれ ガンマ分布とポアソン分布の混合分布， 指数分布とポアソン分布の混合分布であることを示します。 (flyioさんのブログ を参考にさせていただきました。) まず，ガンマ分布とポアソン分布の混合分布 (ポアソン分布のパラメータ\(\lambda\)がガンマ分布に従うときの分布)を 計算してみます。

\[ \begin{aligned} & \int_0^\infty \text{Poisson}(x|\lambda) \text{Gamma}(\lambda|a,b) d \lambda \\ &= \int_0^\infty \frac{\lambda^x}{x!} e^{-\lambda} \frac{b^a}{\Gamma (a)} \lambda^{a - 1} e^{-b \lambda} d \lambda \\ &= \frac{b^a}{x! \Gamma (a)} \int_0^\infty \lambda^{x + a - 1} e^{-\lambda(1 + b)} d \lambda \\ & (ここで，\mu = \lambda (1 + b), d \lambda = \frac{d \mu}{1+b} とします。) \\ &= \frac{b^a}{x! \Gamma (a)} \int_0^\infty \left( \frac{\mu}{1+b} \right)^{x + a - 1} e^{-\mu} \frac{d \mu}{1 + b} \\ &= \frac{b^a}{x! \Gamma (a) (1+b)^{x+a}} \int_0^\infty \mu^{x + a - 1} e^{-\mu} d \mu \\ & (ガンマ関数の定義 \Gamma(x) = \int_0^\infty \mu^{x - 1} e^{-\mu} d \mu より) \\ &= \frac{b^a}{x! \Gamma (a) (1+b)^{x+a}} \Gamma (x + a) \\ &= \frac{\Gamma (x + a)}{\Gamma (a) x!} b^a (1+b)^{-x - a} \\ & (ここで，b = \frac{p}{1-p}とおくと) \\ &= \frac{\Gamma (x + a)}{\Gamma (a) x!} \left(\frac{p}{1-p} \right)^a \left(\frac{1}{1-p} \right)^{-x - a} \\ &= \frac{\Gamma (x + a)}{\Gamma (a) x!} p^a (1-p)^x \end{aligned} \] 最後の式は負の二項分布の定義式 (\(n \to a\)としたもの) そのものです。

なお，この式に\(a = 1\)を代入すると， \[ \begin{aligned} & \frac{\Gamma (x + 1)}{\Gamma(x+1) 1!} p (1-p)^x \\ &= p (1-p)^x \end{aligned} \] となり，これは幾何分布の式になります。

そのとき対応するガンマ分布は， \[ \text{Gamma}(\lambda|a = 1,b) = \frac{b}{\Gamma (1)} \lambda^{0} e^{-b \lambda} = b e^{-b \lambda} \] となりますが，これは\(b\)をパラメータとする指数分布です。