実データ (Johnson-300) の解析: 回答ミスがある回答者の分析
準備
必要なパッケージを読み込みます。
library(psych)
library(GPArotation)
library(tidyverse)
library(GGally)Gerlachらは無回答項目が1項目でもある 回答者は解析から除外していました。実は, そういう回答者は全体の半分以上います。それでも IPIP-NEO-300では完全回答した回答者が15万人近くいるので,十分なサンプル数は得られるのですが,そこには 「300項目もの質問にもれなく回答できる人」というサンプリングバイアスが 働いているのではないか,と気になります。 例えば,そういう人は誠実性が高い,という可能性はないでしょうか。
ここでは,IPIP-NEO-300に関して,無回答項目がある回答者についても 同じ因子分析モデルを用いて因子スコアを求め, 完全な回答者との間で何か違いがないか確認してみます。
ここでは基本的には実データ (Johnson-300) の解析1の流れ に沿って分析します。
データの読み込み
nmax <- Inf # 読み込む最大行数 最初は小さくして試す
dat.raw <- scan(file = "C:/data/personality/IPIP300.dat",
nmax = nmax, what = character(), sep = "\n")
n.data <- length(dat.raw)
dat.matrix <- matrix(0, nrow = n.data, ncol = 300)
n.used.data <- 0
# 回答ミスの数を記録する配列
count.miss <- numeric(n.data)
for (idx in 1:n.data){
# 回答があるのは34列目から333列目
# そこを抜き出す
tmp <- substring(dat.raw[[idx]],34, 333)
tmp.numeric <- as.numeric( unlist(strsplit(tmp,"")))
count.miss[idx] <- sum(tmp.numeric == 0)
n.used.data <- n.used.data + 1
dat.matrix[n.used.data,] <- tmp.numeric
# 無回答は0になっているので,NAに
tmp.numeric[tmp.numeric == 0] <- NA
}
# 不要な行は削除
df_data <- as.data.frame(dat.matrix[1:n.used.data,])
cat("無回答項目無し回答者数:", sum(count.miss == 0),
" 無回答項目有り回答者数:", sum(count.miss > 0), "\n")## 無回答項目無し回答者数: 145388 無回答項目有り回答者数: 161925後で無回答項目数のモデリングに使うため,無回答項目数を 保存しておきます。
write.csv(data.frame(count.miss), "./data_count_miss_IPIP300.csv",
row.names = FALSE)無回答項目数の分布をチェックする
無回答項目数の分布を見てみます。
barplot(table(count.miss),
xlab = "Number of missed items", ylab = "Frequency")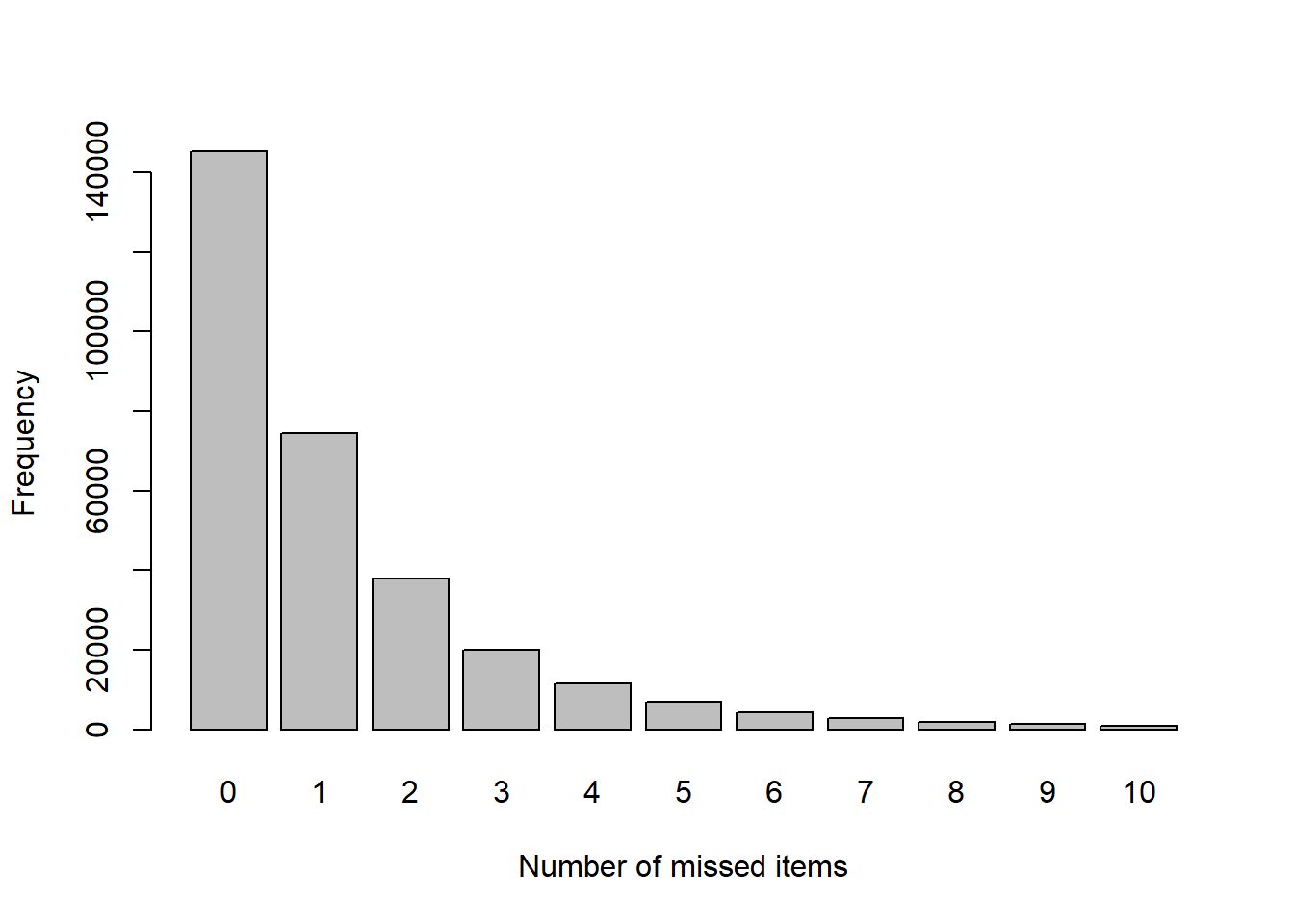
無回答項目が無い回答者が一番多く,そこから無回答項目の数が増えるごとに 回答者はほぼ半分ずつ,指数関数的に減少しているようです。
ここで,どの回答者もすべて同じだけの確率で回答ミスを犯す という可能性がないか考えてみます。回答ミスがなかった回答者は たまたまミスをしなかっただけで,その特性は回答ミスをした回答者と何ら 変わらない,という可能性です。もしそれが事実だとすると, 回答ミスがあった回答者がそうでない回答者とパーソナリティにおいて も何か違いがある,ということはあまり期待できません。
回答ミスをする確率がどの質問項目,どの回答者も 一定であり,これを\(\lambda/300\) とすると(300は項目数), 個人ごとの無回答項目数の分布はパラメータ\(\lambda\)の ポアソン分布に近似的に従います (例えば こちらを参照)。
ポアソン分布をこの無回答項目数にフィットしてみましょう。 上の無回答項目から最尤推定でフィットしたポアソン分布を実線と〇で示します。
# ポアソン分布の最尤推定値はデータの平均値
lambda_est <- mean(count.miss)
mp <- barplot(table(count.miss)/length(count.miss),
xlab = "Number of missed items", ylab = "probability")
lines(mp, dpois(0:10, lambda_est),type = "o")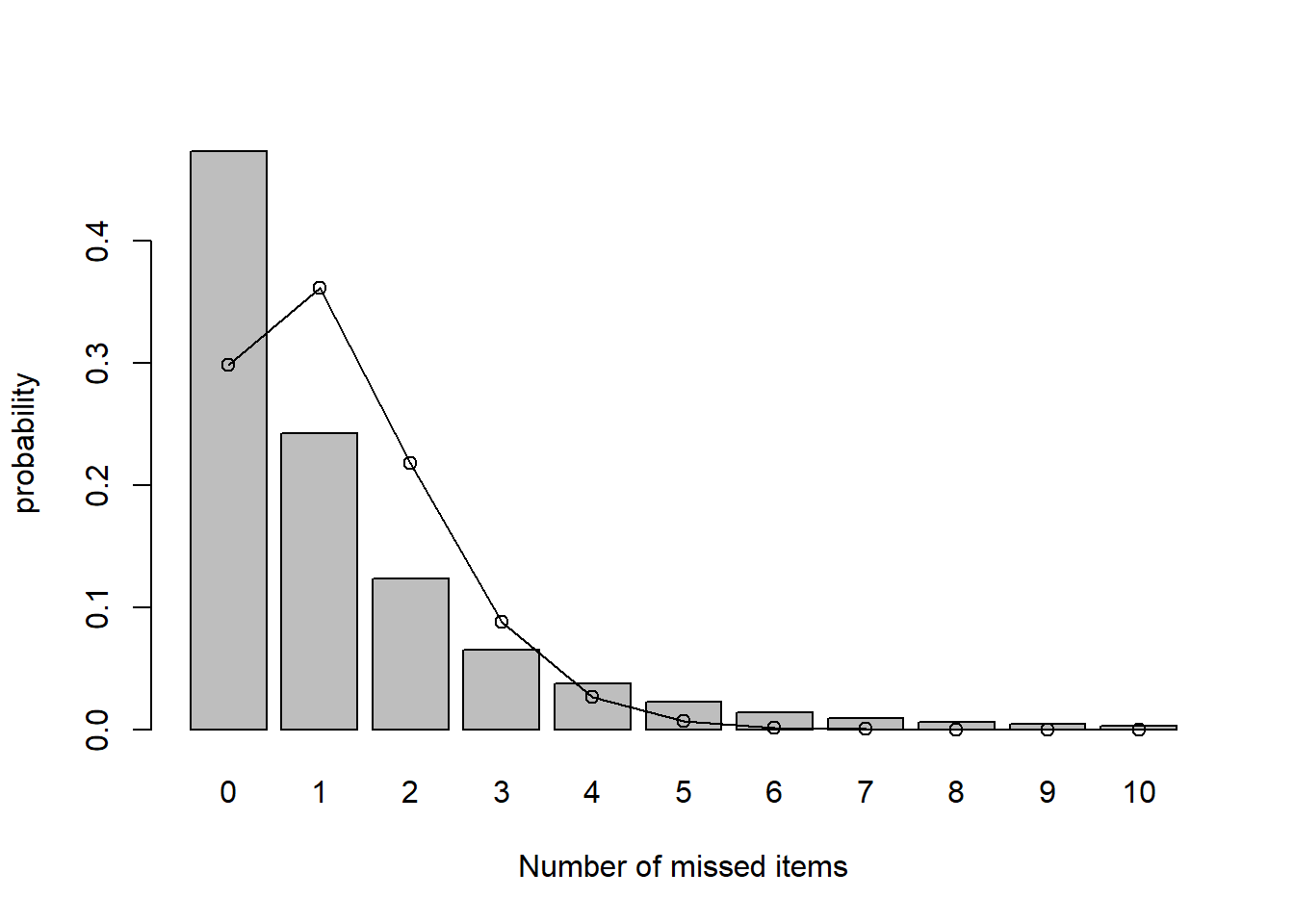
明らかにポアソン分布はこのデータには当てはまっていません。 全回答者がそれぞれの項目で独立に同じ確率で回答ミスをしていたと 考えるには,回答ミスがゼロの回答者が多すぎるようです。 やはり,回答ミスを全くしない回答者と多少でもする回答者は 回答ミスをする確率が異なるのかもしれません (回答ミス数のモデリングについては回答ミス数のモデリングを参照してください)。 ここでは, 少なくとも回答ミスの全くない回答者とそうでない回答者が何か違うかもしれないという 可能性が示唆されたので,パーソナリティにも違いがあるか見ていきましょう。
因子負荷,因子スコアの推定
データの項目 (列) の順番を, “N”の項目 (1, 5, 10,…,296), “E”の項目(2, 6, 11,…,297), “O”の項目(3, 7, 12,…,298), “A”の項目(4, 8, 13,…,299),
“C”の項目(5, 9, 14,…,300), の順番になるよう列を並び替えます。
# 並べ替えのためのインデックス
idxseq <- c(seq(1,296, by=5), # N
seq(2,297, by=5), # E
seq(3,298, by=5), # O
seq(4,299, by=5), # A
seq(5,300, by=5) # C
)
df_data <- df_data[,idxseq]完全データを用いて最尤法とバリマックス回転で因子分析を行い,推定された因子スコアをデータフレームdf_scに格納します。 因子スコアの推定には,これまで使っていた Hermanの方法は欠損値があるとエラーが出るようなので,ここではAnderson and Rubinの方法を用います。 オプションmissingをTRUEにすることで, 欠損データは平均値で補間してから推定が行われます。
res_fa <- fa(df_data, nfactors = 5,
rotate = "varimax",
scores = "Anderson",
fm = "ml", missing = TRUE)
df_sc <- data.frame(res_fa$scores)因子の解釈
因子負荷は以下のようになります。
cor.plot(res_fa, numbers = F)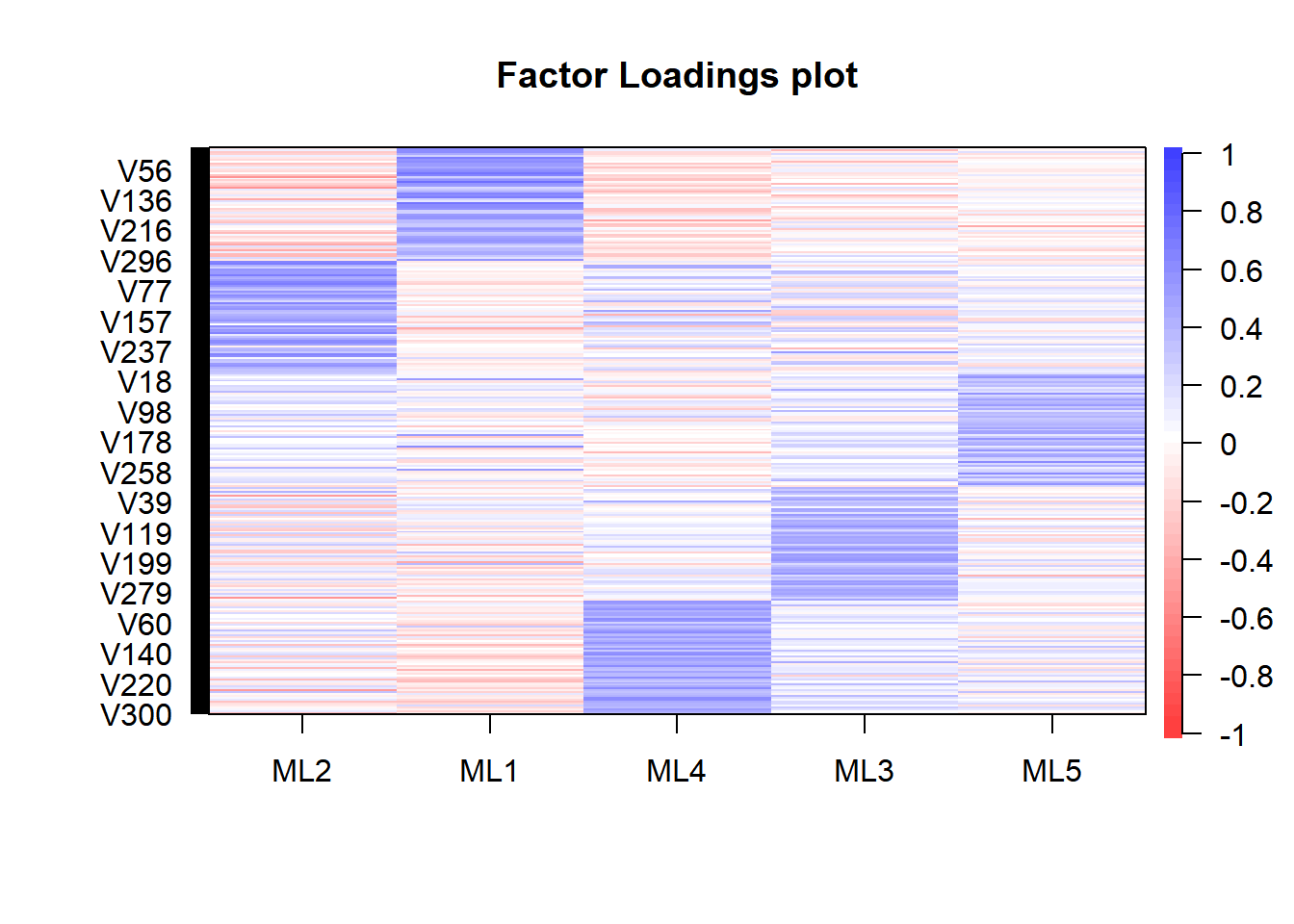
これをもとに推定された因子スコアにラベルを付けます。
names(df_sc) <- c("E","N","C","A","O")
df_sc <- df_sc[,c("N","E","O","A","C")]
df_sc <- df_sc %>% mutate(miss = count.miss > 0)
df_sc$miss <- as.factor(df_sc$miss)因子スコアの比較
回答ミスの有無で各因子スコアの周辺分布を比較してみます。
df_sc_g <- df_sc %>% tidyr::gather(key = domain,
value = factor.score, -miss)
g <- ggplot(df_sc_g, aes(x=factor.score)) +
geom_density(aes(colour=miss, fill=miss,
linetype=miss), alpha = 0.3) +
facet_grid(domain~.)
g
回答ミスなしの回答者 (ピンク)と 回答ミスありの回答者 (緑)の分布は概ね重なっています。 しいて言えば,開放性 (O)はミスのない回答者の分布がわずかに右に寄っているようです。
2次元の周辺分布も見てみましょう。
ggp <- ggpairs(df_sc, aes(colour=miss, alpha = 0.5),
upper = list(continuous='blank'),
lower=list(continuous='density') )
print(ggp)